Jelaskan aspek intelegensi manakah yang berkaitan dengan minat matematika – Siapa yang tidak suka dengan matematika? Di balik rumus dan angka-angka yang terkadang rumit, matematika menyimpan pesona tersendiri. Tapi tahukah Anda bahwa kemampuan kita dalam memahami dan menyukai matematika tidak hanya ditentukan oleh kecerdasan saja, melainkan juga oleh beberapa aspek intelegensi yang saling terkait?
Dalam artikel ini, kita akan menjelajahi beberapa aspek intelegensi yang berperan penting dalam minat dan kemampuan seseorang dalam mempelajari matematika. Mulai dari kemampuan bernalar logis hingga kemampuan visualisasi dan manipulasi spasial, semua aspek ini saling melengkapi dalam membentuk kecakapan matematika.
Aspek Intelegensi Logika-Matematika

Matematika merupakan bidang ilmu yang menuntut kemampuan berpikir logis, sistematis, dan abstrak. Kemampuan ini terkait erat dengan aspek intelegensi logika-matematika, yang merupakan salah satu dari berbagai jenis kecerdasan yang diusulkan oleh teori Multiple Intelligences oleh Howard Gardner.
Kemampuan Bernalar Deduktif dan Induktif
Kemampuan bernalar deduktif dan induktif adalah kunci dalam memahami konsep matematika. Bernalar deduktif melibatkan pengambilan kesimpulan yang spesifik dari premis umum. Misalnya, jika kita mengetahui bahwa semua segitiga memiliki tiga sisi, dan kita memiliki bentuk dengan tiga sisi, maka kita dapat menyimpulkan bahwa bentuk tersebut adalah segitiga. Sebaliknya, bernalar induktif melibatkan pengambilan kesimpulan umum dari pengamatan spesifik. Misalnya, jika kita melihat beberapa segitiga dan menemukan bahwa semua segitiga memiliki sudut yang berjumlah 180 derajat, kita dapat menyimpulkan bahwa semua segitiga memiliki sudut yang berjumlah 180 derajat.
Kemampuan Memecahkan Masalah Secara Sistematis dan Logis
Matematika seringkali melibatkan pemecahan masalah yang membutuhkan pendekatan sistematis dan logis. Contohnya, ketika kita ingin menghitung luas persegi panjang, kita perlu mengikuti langkah-langkah tertentu, seperti mengukur panjang dan lebarnya, lalu mengalikan keduanya. Kemampuan untuk mengidentifikasi langkah-langkah yang diperlukan, mengatur urutannya secara logis, dan menerapkannya dengan tepat sangat penting dalam memecahkan masalah matematika.
Kemampuan Berpikir Abstrak dan Simbolis
Matematika melibatkan konsep-konsep abstrak yang diwakili oleh simbol-simbol. Misalnya, angka “2” mewakili konsep abstrak dari dua buah objek, dan simbol “+” mewakili operasi penjumlahan. Kemampuan untuk memahami dan memanipulasi simbol-simbol ini, serta untuk berpikir abstrak tentang konsep-konsep yang diwakilinya, sangat penting dalam pemahaman matematika.
Perbandingan Aspek Intelegensi Logika-Matematika dengan Aspek Lainnya
| Aspek Intelegensi | Karakteristik | Contoh |
|---|---|---|
| Logika-Matematika | Kemampuan bernalar logis, memecahkan masalah, berpikir sistematis, dan memahami konsep abstrak. | Menghitung, memecahkan persamaan, membuktikan teorema. |
| Bahasa | Kemampuan memahami, menggunakan, dan memanipulasi bahasa. | Membaca, menulis, berbicara, mendengarkan. |
| Musikal | Kemampuan memahami, menciptakan, dan merespons musik. | Bernyanyi, memainkan alat musik, mengaransemen musik. |
| Kinestetik | Kemampuan mengontrol gerakan tubuh dan koordinasi. | Menari, berolahraga, melakukan operasi bedah. |
| Spasial | Kemampuan memahami dan memanipulasi ruang dan bentuk. | Membuat peta, merancang bangunan, bermain catur. |
| Interpersonal | Kemampuan memahami dan berinteraksi dengan orang lain. | Memimpin, bernegosiasi, membangun hubungan. |
| Intrapersonal | Kemampuan memahami diri sendiri dan mengelola emosi. | Merenungkan, menetapkan tujuan, mengembangkan kesadaran diri. |
| Naturalis | Kemampuan memahami dan berinteraksi dengan alam. | Menanam tanaman, mengamati hewan, mempelajari ilmu alam. |
Aspek Intelegensi Spasial
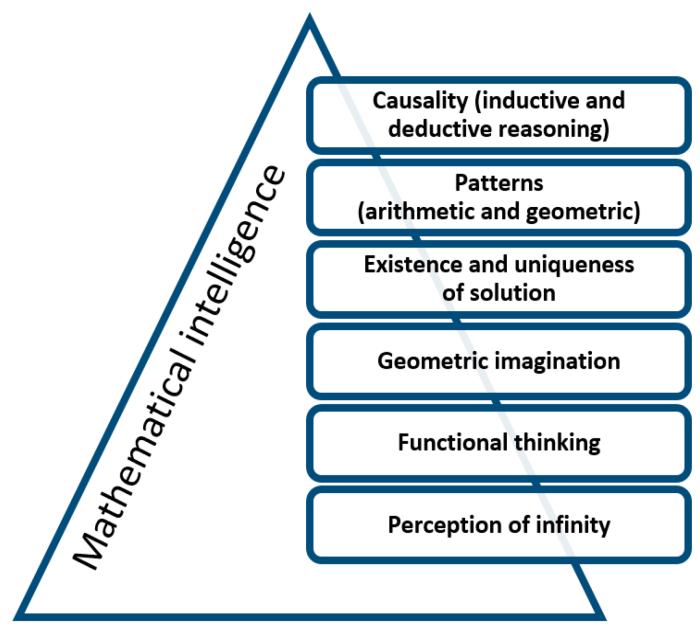
Minat dan kemampuan dalam matematika tidak hanya ditentukan oleh kecerdasan logika-matematika, tetapi juga dipengaruhi oleh aspek intelegensi lainnya. Salah satunya adalah intelegensi spasial, yang berperan penting dalam memahami konsep-konsep matematika yang melibatkan ruang dan bentuk.
Kemampuan Visualisasi dan Manipulasi Objek Spasial
Kemampuan visualisasi dan manipulasi objek spasial memungkinkan seseorang untuk “melihat” dan “mengoperasikan” objek dalam pikiran mereka. Dalam konteks matematika, kemampuan ini sangat membantu dalam memahami geometri. Misalnya, ketika mempelajari bentuk tiga dimensi seperti kubus, seseorang dengan intelegensi spasial yang tinggi dapat dengan mudah membayangkan bentuk tersebut dari berbagai sudut pandang dan memvisualisasikan bagaimana bentuk tersebut dapat diubah atau diputar.
Kemampuan Mengidentifikasi Pola dan Hubungan Spasial
Kemampuan mengidentifikasi pola dan hubungan spasial sangat penting dalam menyelesaikan soal matematika yang melibatkan bentuk dan ruang. Misalnya, dalam soal geometri, seseorang dengan kemampuan spasial yang baik dapat dengan mudah mengenali pola dalam susunan bentuk dan memahami hubungan antar bentuk tersebut. Kemampuan ini juga membantu dalam memahami konsep-konsep seperti simetri dan transformasi geometri.
Kemampuan Berorientasi Spasial
Kemampuan berorientasi spasial memungkinkan seseorang untuk memahami posisi dan arah objek dalam ruang. Dalam matematika, kemampuan ini membantu dalam memahami konsep-konsep yang melibatkan ruang dan bentuk, seperti koordinat, vektor, dan transformasi geometri. Misalnya, seseorang dengan kemampuan berorientasi spasial yang baik dapat dengan mudah memahami konsep koordinat Cartesian dan bagaimana titik-titik dalam ruang dapat diwakili oleh koordinat tersebut.
Sebagai ilustrasi, kemampuan spasial membantu dalam memahami konsep luas dan volume. Bayangkan sebuah persegi panjang. Seseorang dengan kemampuan spasial yang tinggi dapat dengan mudah membayangkan luas persegi panjang tersebut sebagai jumlah kotak-kotak kecil yang dapat mengisi persegi panjang tersebut. Begitu pula dengan volume, mereka dapat membayangkan jumlah kubus kecil yang dapat mengisi sebuah kubus.
Aspek Intelegensi Linguistik: Jelaskan Aspek Intelegensi Manakah Yang Berkaitan Dengan Minat Matematika

Kemampuan memahami dan menggunakan bahasa, atau intelegensi linguistik, ternyata punya peran penting dalam mempelajari matematika. Mungkin kamu berpikir matematika itu hanya soal angka dan rumus, tapi nyatanya kemampuan berbahasa juga ikut berperan dalam menguasai bidang ini.
Memahami dan Menggunakan Bahasa dalam Matematika
Bayangkan kamu sedang membaca soal cerita matematika. Untuk menyelesaikan soal tersebut, kamu perlu memahami makna setiap kata dan kalimatnya. Kemampuan memahami bahasa membantu kamu dalam menafsirkan soal cerita dan mengidentifikasi informasi yang diperlukan untuk menyelesaikannya.
Menerjemahkan Simbol dan Rumus Matematika
Simbol dan rumus matematika bisa diibaratkan sebagai bahasa khusus dalam dunia matematika. Kemampuan mengartikan simbol dan rumus ini sangat penting untuk memahami konsep matematika dan menyelesaikan masalah.
- Misalnya, simbol “+” berarti penjumlahan, “-” berarti pengurangan, dan “x” berarti perkalian. Dengan memahami arti simbol-simbol tersebut, kamu bisa menghitung dan menyelesaikan persamaan matematika dengan lebih mudah.
- Rumus matematika, seperti rumus luas persegi panjang (L = p x l), juga merupakan bentuk bahasa yang membantu kita memahami hubungan antara variabel-variabel dalam matematika.
Mengelola Informasi Secara Logis
Kemampuan mengorganisasikan dan menyusun informasi secara logis juga sangat penting dalam mempelajari matematika. Matematika adalah ilmu yang terstruktur dan sistematis.
- Dalam menyelesaikan masalah matematika, kamu perlu menyusun langkah-langkah penyelesaian secara logis dan terstruktur.
- Kemampuan memahami hubungan sebab-akibat dalam matematika juga penting.
Hubungan Kemampuan Linguistik dan Matematika
| Kemampuan Linguistik | Kemampuan Matematika |
|---|---|
| Memahami makna kata dan kalimat | Menafsirkan soal cerita matematika |
| Menerjemahkan simbol dan rumus | Memahami konsep matematika |
| Menyusun informasi secara logis | Menyelesaikan masalah matematika |
Aspek Intelegensi Interpersonal
Kecerdasan interpersonal, atau kemampuan untuk memahami dan berinteraksi dengan orang lain, ternyata memiliki peran penting dalam memahami matematika. Meskipun matematika sering dianggap sebagai bidang yang individual, kemampuan interpersonal dapat membantu dalam membangun pemahaman yang lebih dalam dan membangun lingkungan belajar yang positif.
Bekerja Sama dan Berkolaborasi
Bekerja sama dan berkolaborasi dengan orang lain dalam matematika dapat membuka perspektif baru dan membantu memecahkan masalah dengan lebih efektif. Saat bekerja dalam kelompok, individu dapat berbagi ide, strategi, dan perspektif yang berbeda, yang dapat mengarah pada solusi yang lebih kreatif dan komprehensif. Diskusi kelompok juga dapat membantu mengklarifikasi konsep yang sulit dan mengidentifikasi kesalahpahaman.
Komunikasi dan Penjelasan Konsep
Kemampuan berkomunikasi dan menjelaskan konsep matematika kepada orang lain dapat meningkatkan pemahaman seseorang. Ketika kita berusaha untuk menjelaskan suatu konsep kepada orang lain, kita dipaksa untuk meninjau dan mengorganisir pemikiran kita dengan lebih jelas. Proses ini membantu mengidentifikasi area yang kita pahami dengan baik dan area yang masih membutuhkan klarifikasi. Selain itu, memberi penjelasan kepada orang lain juga membantu kita untuk memahami konsep tersebut dari sudut pandang yang berbeda.
Memahami dan Merespons Emosi
Kemampuan untuk memahami dan merespons emosi orang lain sangat penting dalam membangun lingkungan belajar matematika yang positif. Guru yang peka terhadap emosi siswa dapat menciptakan suasana yang mendukung dan memotivasi, di mana siswa merasa nyaman untuk bertanya, berbagi ide, dan mengambil risiko. Lingkungan belajar yang positif dapat meningkatkan kepercayaan diri siswa dan motivasi mereka untuk belajar matematika.
“Kemampuan interpersonal sangat membantu dalam pembelajaran matematika kelompok. Saat kita bekerja sama, kita dapat saling memotivasi, membantu mengatasi kesulitan, dan berbagi strategi pemecahan masalah. Ini menciptakan lingkungan belajar yang kolaboratif dan menyenangkan, di mana semua orang merasa dihargai dan didukung.”
Aspek Intelegensi Intrapersonal
Aspek intrapersonal dalam teori kecerdasan majemuk mengacu pada kemampuan seseorang untuk memahami dirinya sendiri, termasuk perasaan, motivasi, dan kekuatan serta kelemahannya. Kemampuan ini memainkan peran penting dalam proses belajar, terutama dalam memahami konsep matematika yang seringkali kompleks dan membutuhkan pemikiran yang mendalam.
Memahami Diri Sendiri dan Memotivasi Diri Sendiri
Memahami diri sendiri dalam konteks belajar matematika berarti mengenali gaya belajar, preferensi, dan strategi yang paling efektif bagi kita. Misalnya, beberapa orang mungkin lebih suka belajar dengan cara visual, sementara yang lain lebih menyukai pendekatan auditori. Dengan memahami gaya belajar sendiri, kita dapat memilih metode belajar yang paling sesuai dan meningkatkan efektivitasnya. Selain itu, motivasi diri sendiri menjadi kunci dalam menghadapi tantangan matematika. Kemampuan untuk menetapkan tujuan, mengatasi kekecewaan, dan mempertahankan fokus pada pembelajaran sangat penting untuk mencapai kemajuan.
Mengatur Waktu dan Fokus, Jelaskan aspek intelegensi manakah yang berkaitan dengan minat matematika
Matematika seringkali melibatkan menyelesaikan masalah yang membutuhkan konsentrasi dan waktu yang cukup. Kemampuan mengatur waktu dan fokus menjadi sangat penting dalam konteks ini. Dengan mengatur waktu belajar secara efektif, kita dapat memastikan bahwa kita memiliki waktu yang cukup untuk memahami konsep, mengerjakan latihan, dan mengulang materi. Selain itu, fokus yang baik membantu kita untuk menghindari gangguan dan memusatkan perhatian pada tugas yang sedang dikerjakan.
Mengenali Kekuatan dan Kelemahan Diri Sendiri
Mengenali kekuatan dan kelemahan diri sendiri dalam belajar matematika membantu kita untuk fokus pada aspek yang perlu ditingkatkan dan memanfaatkan kekuatan yang sudah dimiliki. Misalnya, jika kita kuat dalam aljabar tetapi lemah dalam geometri, kita dapat mengalokasikan lebih banyak waktu untuk mempelajari geometri dan meminta bantuan tambahan jika diperlukan. Dengan fokus pada area yang membutuhkan peningkatan, kita dapat mencapai kemajuan yang signifikan dalam memahami matematika.
Hubungan Aspek Intrapersonal dengan Strategi Belajar Matematika
| Aspek Intrapersonal | Strategi Belajar Matematika |
|---|---|
| Memahami Diri Sendiri | Memilih metode belajar yang sesuai dengan gaya belajar individu, seperti visual, auditori, atau kinestetik. |
| Memotivasi Diri Sendiri | Menetapkan tujuan yang realistis, memberikan penghargaan atas kemajuan, dan menghindari perbandingan dengan orang lain. |
| Mengatur Waktu dan Fokus | Membuat jadwal belajar yang teratur, memilih tempat belajar yang tenang, dan menghindari gangguan selama belajar. |
| Mengenali Kekuatan dan Kelemahan Diri Sendiri | Fokus pada area yang membutuhkan peningkatan, meminta bantuan tambahan jika diperlukan, dan memanfaatkan kekuatan yang sudah dimiliki. |
Penutupan Akhir
Memahami aspek-aspek intelegensi yang berperan dalam minat matematika membuka peluang bagi kita untuk mengembangkan kemampuan dan potensi diri dalam bidang ini. Dengan mengenali kekuatan dan kelemahan diri, kita dapat memilih strategi belajar yang efektif dan menemukan cara terbaik untuk memahami dan mengapresiasi matematika.







