Contoh soal logaritma dan pembahasannya – Logaritma, sebuah konsep matematika yang mungkin terdengar asing bagi sebagian orang, ternyata punya peran penting dalam berbagai bidang, lho! Dari menghitung kekuatan gempa bumi hingga menganalisis pertumbuhan ekonomi, logaritma hadir untuk mempermudah pemahaman kita tentang dunia.
Dalam artikel ini, kita akan menjelajahi dunia logaritma dengan mempelajari definisi, sifat, dan berbagai contoh soal logaritma beserta pembahasannya. Siap-siap untuk mengasah kemampuan matematika dan mengungkap rahasia di balik logaritma!
Pengertian Logaritma
Logaritma merupakan konsep matematika yang erat kaitannya dengan eksponen. Sederhananya, logaritma adalah operasi matematika yang mencari pangkat (eksponen) dari suatu bilangan dasar (basis) untuk mendapatkan nilai tertentu. Dengan kata lain, logaritma menjawab pertanyaan “berapa pangkat yang harus kita berikan pada suatu bilangan dasar untuk mendapatkan nilai tertentu?”.
Contoh Logaritma dalam Kehidupan Sehari-hari
Sebagai contoh, bayangkan Anda menabung sejumlah uang di bank dengan bunga majemuk. Setiap tahun, jumlah tabungan Anda akan meningkat secara eksponensial. Untuk mengetahui berapa lama waktu yang dibutuhkan agar tabungan Anda mencapai nilai tertentu, Anda dapat menggunakan konsep logaritma.
Misalnya, jika Anda menabung Rp1.000.000,- dengan bunga 10% per tahun, dan ingin mengetahui berapa tahun yang dibutuhkan agar tabungan Anda mencapai Rp2.000.000,-. Maka, Anda dapat menggunakan logaritma untuk menghitungnya.
Hubungan Logaritma, Eksponen, dan Basis
Berikut tabel yang menunjukkan hubungan antara logaritma, eksponen, dan basis:
| Basis | Eksponen | Nilai | Logaritma |
|---|---|---|---|
| 2 | 3 | 8 | log2 8 = 3 |
| 10 | 2 | 100 | log10 100 = 2 |
| 5 | 4 | 625 | log5 625 = 4 |
Dalam tabel di atas, kolom “Logaritma” menunjukkan bagaimana kita menyatakan logaritma dari suatu nilai. Misalnya, “log2 8 = 3″ dibaca “logaritma 8 dengan basis 2 sama dengan 3”. Ini berarti 2 pangkat 3 sama dengan 8.
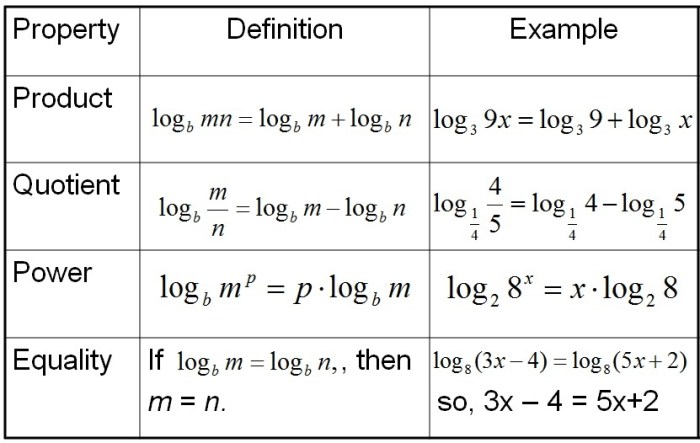
Sifat-Sifat Logaritma
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen. Sifat-sifat logaritma sangat penting dalam menyelesaikan persamaan logaritma dan menyederhanakan operasi logaritma.
Sifat-Sifat Penting Logaritma, Contoh soal logaritma dan pembahasannya
Sifat-sifat logaritma memudahkan kita dalam melakukan operasi matematika yang melibatkan logaritma. Berikut adalah beberapa sifat penting logaritma:
- Sifat Perkalian: loga (x * y) = loga x + loga y. Sifat ini menyatakan bahwa logaritma dari hasil kali dua bilangan sama dengan jumlah logaritma dari masing-masing bilangan tersebut.
- Sifat Pembagian: loga (x / y) = loga x – loga y. Sifat ini menyatakan bahwa logaritma dari hasil bagi dua bilangan sama dengan selisih logaritma dari masing-masing bilangan tersebut.
- Sifat Pangkat: loga xn = n * loga x. Sifat ini menyatakan bahwa logaritma dari bilangan yang dipangkatkan sama dengan hasil kali pangkat dengan logaritma dari bilangan tersebut.
- Sifat Basis: loga a = 1. Sifat ini menyatakan bahwa logaritma dari suatu bilangan dengan basis yang sama dengan bilangan tersebut selalu bernilai 1.
- Sifat Basis 1: loga 1 = 0. Sifat ini menyatakan bahwa logaritma dari 1 dengan basis berapa pun selalu bernilai 0.
Penerapan Sifat Logaritma dalam Menyelesaikan Persamaan Logaritma
Sifat-sifat logaritma dapat digunakan untuk menyelesaikan persamaan logaritma. Contohnya, untuk menyelesaikan persamaan log2 (x + 1) + log2 (x – 1) = 3, kita dapat menggunakan sifat perkalian logaritma:
log2 (x + 1) + log2 (x – 1) = 3
log2 [(x + 1)(x – 1)] = 3
log2 (x2 – 1) = 3
x2 – 1 = 23
x2 – 1 = 8
x2 = 9
x = ±3
Oleh karena itu, solusi dari persamaan tersebut adalah x = 3 dan x = -3.
Penggunaan Sifat Logaritma untuk Menyederhanakan Operasi Logaritma
Sifat-sifat logaritma juga dapat digunakan untuk menyederhanakan operasi logaritma. Misalnya, untuk menyederhanakan ekspresi log3 27 + log3 9, kita dapat menggunakan sifat perkalian logaritma:
log3 27 + log3 9 = log3 (27 * 9) = log3 243 = 5
Dengan menggunakan sifat-sifat logaritma, kita dapat menyederhanakan operasi logaritma dan menyelesaikan persamaan logaritma dengan lebih mudah.
Persamaan Logaritma: Contoh Soal Logaritma Dan Pembahasannya
Persamaan logaritma adalah persamaan yang memuat variabel dalam bentuk logaritma. Untuk menyelesaikan persamaan logaritma, kita perlu memanfaatkan sifat-sifat logaritma dan operasi aljabar.
Pengertian Persamaan Logaritma
Persamaan logaritma adalah persamaan yang memuat variabel dalam bentuk logaritma. Secara sederhana, persamaan logaritma adalah persamaan yang menyatakan hubungan antara logaritma suatu bilangan dengan variabel.
Contoh Soal Persamaan Logaritma
Berikut adalah beberapa contoh soal persamaan logaritma dengan berbagai bentuk:
Contoh 1: Persamaan Logaritma Sederhana
Tentukan nilai x yang memenuhi persamaan:
log2 (x + 1) = 3
Contoh 2: Persamaan Logaritma dengan Koefisien
Tentukan nilai x yang memenuhi persamaan:
2 log3 (x – 2) = 4
Contoh 3: Persamaan Logaritma dengan Basis Berbeda
Tentukan nilai x yang memenuhi persamaan:
log2 (x) + log3 (x) = 5
Contoh 4: Persamaan Logaritma dengan Eksponen
Tentukan nilai x yang memenuhi persamaan:
log2 (x2 + 1) = 4
Langkah-Langkah Menyelesaikan Persamaan Logaritma
Untuk menyelesaikan persamaan logaritma, kita dapat menggunakan sifat-sifat logaritma dan operasi aljabar. Berikut adalah langkah-langkah umum yang dapat digunakan:
- Ubah persamaan logaritma ke bentuk eksponensial.
- Sederhanakan persamaan menggunakan operasi aljabar.
- Tentukan nilai variabel yang memenuhi persamaan.
- Verifikasi solusi dengan substitusi nilai variabel ke dalam persamaan logaritma asli.
Contoh Pembahasan Persamaan Logaritma
Berikut adalah contoh pembahasan untuk menyelesaikan persamaan logaritma:
Contoh 1: Persamaan Logaritma Sederhana
log2 (x + 1) = 3
Ubah persamaan logaritma ke bentuk eksponensial:
23 = x + 1
Sederhanakan persamaan:
8 = x + 1
Tentukan nilai x:
x = 7
Verifikasi solusi dengan substitusi nilai x ke dalam persamaan logaritma asli:
log2 (7 + 1) = log2 8 = 3
Jadi, nilai x yang memenuhi persamaan adalah x = 7.
Contoh 2: Persamaan Logaritma dengan Koefisien
2 log3 (x – 2) = 4
Sederhanakan persamaan:
log3 (x – 2) = 2
Ubah persamaan logaritma ke bentuk eksponensial:
32 = x – 2
Sederhanakan persamaan:
9 = x – 2
Tentukan nilai x:
x = 11
Verifikasi solusi dengan substitusi nilai x ke dalam persamaan logaritma asli:
2 log3 (11 – 2) = 2 log3 9 = 2 x 2 = 4
Jadi, nilai x yang memenuhi persamaan adalah x = 11.
Contoh 3: Persamaan Logaritma dengan Basis Berbeda
log2 (x) + log3 (x) = 5
Persamaan ini lebih kompleks karena memiliki basis logaritma yang berbeda. Untuk menyelesaikannya, kita dapat menggunakan sifat-sifat logaritma dan operasi aljabar.
Langkah pertama, kita perlu mengubah kedua logaritma ke basis yang sama. Misalnya, kita dapat mengubah logaritma basis 3 ke basis 2 menggunakan rumus perubahan basis:
loga b = logc b / logc a
Maka, persamaan tersebut menjadi:
log2 (x) + log2 (x) / log2 (3) = 5
Sederhanakan persamaan:
log2 (x) * (1 + 1/log2(3)) = 5
log2 (x) * (log2(3) + 1) / log2(3) = 5
log2 (x) * (log2(3) + 1) = 5 * log2(3)
log2 (x) = (5 * log2(3)) / (log2(3) + 1)
Ubah persamaan logaritma ke bentuk eksponensial:
2(5 * log2(3)) / (log2(3) + 1) = x
Jadi, nilai x yang memenuhi persamaan adalah x = 2(5 * log2(3)) / (log2(3) + 1).
Contoh 4: Persamaan Logaritma dengan Eksponen
log2 (x2 + 1) = 4
Ubah persamaan logaritma ke bentuk eksponensial:
24 = x2 + 1
Sederhanakan persamaan:
16 = x2 + 1
x2 = 15
Tentukan nilai x:
x = ±√15
Verifikasi solusi dengan substitusi nilai x ke dalam persamaan logaritma asli:
log2 ((√15)2 + 1) = log2 (15 + 1) = log2 16 = 4
log2 ((-√15)2 + 1) = log2 (15 + 1) = log2 16 = 4
Jadi, nilai x yang memenuhi persamaan adalah x = √15 dan x = -√15.
Pertidaksamaan Logaritma
Pertidaksamaan logaritma adalah pertidaksamaan yang memuat fungsi logaritma. Fungsi logaritma adalah fungsi invers dari fungsi eksponen. Pertidaksamaan logaritma sering muncul dalam berbagai bidang, seperti matematika, fisika, dan ekonomi.
Definisi Pertidaksamaan Logaritma
Pertidaksamaan logaritma adalah pertidaksamaan yang melibatkan fungsi logaritma. Fungsi logaritma adalah fungsi invers dari fungsi eksponen. Pertidaksamaan logaritma dapat ditulis dalam bentuk:
loga f(x) > g(x)
atau
loga f(x) < g(x)
di mana a adalah basis logaritma, f(x) dan g(x) adalah fungsi dalam x.
Contoh Soal Pertidaksamaan Logaritma
Berikut adalah beberapa contoh soal pertidaksamaan logaritma:
- log2 (x + 1) > 3
- log3 (2x – 1) < 2
- log5 (x2 – 4) > 1
- log4 (x + 2) + log4 (x – 1) > 1
Langkah-langkah Menyelesaikan Pertidaksamaan Logaritma
Berikut adalah langkah-langkah umum untuk menyelesaikan pertidaksamaan logaritma:
- Tentukan domain dari fungsi logaritma. Domain fungsi logaritma adalah himpunan semua bilangan real positif. Dalam contoh soal di atas, domain fungsi logaritma adalah x > -1, x > 1/2, x2 – 4 > 0, dan x + 2 > 0 dan x – 1 > 0.
- Ubah pertidaksamaan logaritma menjadi pertidaksamaan eksponen. Untuk mengubah pertidaksamaan logaritma menjadi pertidaksamaan eksponen, gunakan definisi logaritma. Misalnya, jika loga f(x) > g(x), maka ag(x) < f(x).
- Selesaikan pertidaksamaan eksponen. Pertidaksamaan eksponen dapat diselesaikan dengan menggunakan sifat-sifat eksponen. Misalnya, jika ag(x) < f(x), maka g(x) < loga f(x).
- Tentukan himpunan penyelesaian. Himpunan penyelesaian pertidaksamaan logaritma adalah himpunan semua nilai x yang memenuhi pertidaksamaan tersebut. Pastikan bahwa himpunan penyelesaian terletak di dalam domain fungsi logaritma.
Contoh Soal dan Pembahasan
Berikut adalah contoh soal dan pembahasan pertidaksamaan logaritma:
Contoh Soal 1
Selesaikan pertidaksamaan logaritma berikut:
log2 (x + 1) > 3
Pembahasan
1. Tentukan domain fungsi logaritma:
Domain fungsi logaritma adalah x + 1 > 0, sehingga x > -1.
2. Ubah pertidaksamaan logaritma menjadi pertidaksamaan eksponen:
log2 (x + 1) > 3 => 23 < x + 1
3. Selesaikan pertidaksamaan eksponen:
23 < x + 1 => 8 < x + 1 => 7 < x
4. Tentukan himpunan penyelesaian:
Himpunan penyelesaian pertidaksamaan adalah x > 7. Karena himpunan penyelesaian ini terletak di dalam domain fungsi logaritma, maka himpunan penyelesaian pertidaksamaan adalah x > 7.
Contoh Soal 2
Selesaikan pertidaksamaan logaritma berikut:
log3 (2x – 1) < 2
Pembahasan
1. Tentukan domain fungsi logaritma:
Domain fungsi logaritma adalah 2x – 1 > 0, sehingga x > 1/2.
2. Ubah pertidaksamaan logaritma menjadi pertidaksamaan eksponen:
log3 (2x – 1) < 2 => 32 > 2x – 1
3. Selesaikan pertidaksamaan eksponen:
32 > 2x – 1 => 9 > 2x – 1 => 10 > 2x => 5 > x
4. Tentukan himpunan penyelesaian:
Himpunan penyelesaian pertidaksamaan adalah x < 5. Karena himpunan penyelesaian ini terletak di dalam domain fungsi logaritma, maka himpunan penyelesaian pertidaksamaan adalah 1/2 < x < 5.
Kesimpulan
Pertidaksamaan logaritma merupakan salah satu jenis pertidaksamaan yang melibatkan fungsi logaritma. Untuk menyelesaikan pertidaksamaan logaritma, kita perlu mengubahnya menjadi pertidaksamaan eksponen, kemudian menyelesaikan pertidaksamaan eksponen tersebut. Himpunan penyelesaian pertidaksamaan logaritma adalah himpunan semua nilai x yang memenuhi pertidaksamaan tersebut dan terletak di dalam domain fungsi logaritma.
Fungsi Logaritma
Fungsi logaritma merupakan fungsi invers dari fungsi eksponensial. Fungsi logaritma dapat didefinisikan sebagai berikut:
Jika a > 0 dan a ≠ 1, maka logaritma dengan basis a dari x, dinotasikan sebagai loga x, didefinisikan sebagai eksponen yang harus dipangkatkan a agar menghasilkan x. Dengan kata lain, jika y = loga x, maka ay = x.
Contoh Fungsi Logaritma dan Grafiknya
Sebagai contoh, fungsi logaritma dengan basis 2, yaitu log2 x, memiliki grafik seperti berikut:
[Gambar grafik fungsi logaritma dengan basis 2, dengan sumbu x dan sumbu y, dan titik-titik penting pada grafik ditandai.]
Grafik tersebut menunjukkan bahwa fungsi logaritma dengan basis 2 adalah fungsi monotonik naik, yang berarti bahwa nilai fungsinya selalu meningkat seiring dengan peningkatan nilai x.
Sifat-sifat Fungsi Logaritma
Berikut adalah beberapa sifat penting dari fungsi logaritma:
- Domain: Domain dari fungsi logaritma dengan basis a adalah semua bilangan real positif, yaitu x > 0. Ini karena kita tidak dapat mengambil logaritma dari nol atau bilangan negatif.
- Range: Range dari fungsi logaritma dengan basis a adalah semua bilangan real, yaitu (-∞, ∞). Ini berarti bahwa fungsi logaritma dapat mengambil nilai apa pun.
- Asimtot: Fungsi logaritma memiliki asimtot vertikal di x = 0. Ini berarti bahwa grafik fungsi logaritma mendekati garis vertikal x = 0 tetapi tidak pernah menyentuhnya.
Terakhir
Dengan memahami konsep dasar dan sifat-sifat logaritma, kita dapat dengan mudah menyelesaikan berbagai soal logaritma, baik dalam ujian maupun dalam kehidupan sehari-hari. Logaritma bukanlah hal yang menakutkan, justru merupakan alat yang ampuh untuk memahami dan menyelesaikan berbagai permasalahan kompleks.
Contoh soal logaritma dan pembahasannya bisa kamu temukan di berbagai buku pelajaran atau website. Nah, untuk menguji pemahamanmu tentang konsep fisika, kamu bisa mencoba mengerjakan contoh soal katrol majemuk. Sama seperti logaritma, memahami konsep katrol majemuk akan membantumu menyelesaikan soal-soal yang lebih kompleks.
Jadi, jangan ragu untuk mencoba mengerjakan soal-soal tersebut dan melatih kemampuanmu dalam memecahkan masalah!






