Contoh soal kekongruenan dua segitiga – Pernahkah Anda memperhatikan bahwa dua buah segitiga bisa memiliki bentuk yang sama persis, meskipun ukurannya berbeda? Nah, itulah yang disebut dengan kekongruenan segitiga. Konsep ini menarik, karena mengajarkan kita bagaimana menentukan kesamaan bentuk antara dua segitiga, meskipun mereka mungkin terlihat berbeda pada pandangan pertama.
Dalam artikel ini, kita akan menjelajahi dunia kekongruenan segitiga. Kita akan mempelajari definisi, kriteria, dan contoh soal yang akan membantu Anda memahami konsep ini dengan lebih baik. Siap-siap untuk mengasah kemampuan geometri Anda dan mengungkap misteri kesamaan bentuk!
Pengertian Kekongruenan Dua Segitiga
Dalam geometri, kekongruenan adalah konsep yang menggambarkan kesamaan bentuk dan ukuran dua bangun geometri. Dua bangun geometri dikatakan kongruen jika dapat saling menutupi dengan sempurna tanpa perlu diputar, dibalik, atau diubah ukurannya. Konsep ini sangat penting dalam memahami sifat-sifat geometri dan sering digunakan dalam berbagai bidang seperti arsitektur, desain, dan teknik.
Pengertian Kekongruenan Dua Segitiga
Dua segitiga dikatakan kongruen jika semua sisi dan sudut yang bersesuaian memiliki ukuran yang sama. Artinya, jika kita dapat mencocokkan sisi-sisi dan sudut-sudut dari kedua segitiga tersebut, maka semua pasangan yang bersesuaian akan memiliki ukuran yang sama.
Sebagai ilustrasi, perhatikan gambar berikut:
Segitiga ABC dan segitiga DEF kongruen karena:
- Sisi AB sama dengan sisi DE
- Sisi BC sama dengan sisi EF
- Sisi AC sama dengan sisi DF
- Sudut A sama dengan sudut D
- Sudut B sama dengan sudut E
- Sudut C sama dengan sudut F
Kita dapat menuliskan kongruensi kedua segitiga tersebut sebagai:
△ABC ≅ △DEF
Syarat Kekongruenan Dua Segitiga
Untuk menentukan apakah dua segitiga kongruen, kita tidak perlu memeriksa semua sisi dan sudutnya. Ada beberapa syarat yang dapat digunakan untuk menentukan kekongruenan dua segitiga. Berikut adalah beberapa syarat yang umum digunakan:
- Sisi-Sisi-Sisi (SSS): Dua segitiga dikatakan kongruen jika ketiga sisi yang bersesuaian memiliki ukuran yang sama.
- Sisi-Sudut-Sisi (SAS): Dua segitiga dikatakan kongruen jika dua sisi yang bersesuaian dan sudut yang diapit oleh kedua sisi tersebut memiliki ukuran yang sama.
- Sudut-Sisi-Sudut (ASA): Dua segitiga dikatakan kongruen jika dua sudut yang bersesuaian dan sisi yang diapit oleh kedua sudut tersebut memiliki ukuran yang sama.
- Sudut-Sudut-Sisi (AAS): Dua segitiga dikatakan kongruen jika dua sudut yang bersesuaian dan sisi yang tidak diapit oleh kedua sudut tersebut memiliki ukuran yang sama.
Contoh Dua Segitiga yang Tidak Kongruen
Perhatikan gambar berikut:
Segitiga ABC dan segitiga DEF tidak kongruen karena:
- Sisi AB sama dengan sisi DE
- Sisi BC sama dengan sisi EF
- Sudut A sama dengan sudut D
Meskipun tiga elemen yang bersesuaian memiliki ukuran yang sama, namun sudut B dan sudut E tidak sama. Oleh karena itu, kedua segitiga tersebut tidak memenuhi syarat kekongruenan.
Kriteria Kekongruenan Segitiga
Dalam geometri, dua segitiga dikatakan kongruen jika mereka memiliki bentuk dan ukuran yang sama. Artinya, semua sisi dan sudut yang bersesuaian pada kedua segitiga tersebut memiliki ukuran yang sama. Untuk menentukan apakah dua segitiga kongruen, kita dapat menggunakan beberapa kriteria. Kriteria ini merupakan aturan yang telah terbukti secara matematis dan dapat membantu kita untuk menentukan kekongruenan dua segitiga dengan lebih mudah.
Kriteria Kekongruenan Segitiga, Contoh soal kekongruenan dua segitiga
Berikut adalah tabel yang merangkum kriteria kekongruenan segitiga:
| Kriteria | Syarat | Ilustrasi |
|---|---|---|
| Sisi-Sisi-Sisi (SSS) | Ketiga sisi segitiga yang bersesuaian sama panjang. | Dua segitiga dikatakan kongruen jika ketiga sisi segitiga tersebut memiliki panjang yang sama dengan ketiga sisi segitiga lainnya. Misalnya, jika segitiga ABC memiliki sisi AB = DE, BC = EF, dan AC = DF, maka segitiga ABC kongruen dengan segitiga DEF. |
| Sisi-Sudut-Sisi (SAS) | Dua sisi segitiga yang bersesuaian sama panjang dan sudut yang diapit oleh kedua sisi tersebut sama besar. | Dua segitiga dikatakan kongruen jika dua sisi yang bersesuaian sama panjang dan sudut yang diapit oleh kedua sisi tersebut sama besar. Misalnya, jika segitiga ABC memiliki sisi AB = DE, BC = EF, dan sudut B = sudut E, maka segitiga ABC kongruen dengan segitiga DEF. |
| Sudut-Sisi-Sudut (SAS) | Dua sudut segitiga yang bersesuaian sama besar dan sisi yang diapit oleh kedua sudut tersebut sama panjang. | Dua segitiga dikatakan kongruen jika dua sudut yang bersesuaian sama besar dan sisi yang diapit oleh kedua sudut tersebut sama panjang. Misalnya, jika segitiga ABC memiliki sudut A = sudut D, sudut B = sudut E, dan sisi AB = DE, maka segitiga ABC kongruen dengan segitiga DEF. |
Kriteria Sisi-Sisi-Sisi (SSS)
Kriteria sisi-sisi-sisi (SSS) menyatakan bahwa dua segitiga dikatakan kongruen jika ketiga sisi segitiga tersebut memiliki panjang yang sama dengan ketiga sisi segitiga lainnya.
“Jika ketiga sisi segitiga satu sama panjang dengan ketiga sisi segitiga lainnya, maka kedua segitiga tersebut kongruen.”
Misalnya, perhatikan segitiga ABC dan segitiga DEF di bawah ini:
Jika AB = DE, BC = EF, dan AC = DF, maka segitiga ABC kongruen dengan segitiga DEF berdasarkan kriteria SSS.
Kriteria Sisi-Sudut-Sisi (SAS)
Kriteria sisi-sudut-sisi (SAS) menyatakan bahwa dua segitiga dikatakan kongruen jika dua sisi yang bersesuaian sama panjang dan sudut yang diapit oleh kedua sisi tersebut sama besar.
“Jika dua sisi segitiga satu sama panjang dengan dua sisi segitiga lainnya, dan sudut yang diapit oleh kedua sisi tersebut sama besar, maka kedua segitiga tersebut kongruen.”
Misalnya, perhatikan segitiga ABC dan segitiga DEF di bawah ini:
Jika AB = DE, BC = EF, dan sudut B = sudut E, maka segitiga ABC kongruen dengan segitiga DEF berdasarkan kriteria SAS.
Kriteria Sudut-Sisi-Sudut (SAS)
Kriteria sudut-sisi-sudut (SAS) menyatakan bahwa dua segitiga dikatakan kongruen jika dua sudut yang bersesuaian sama besar dan sisi yang diapit oleh kedua sudut tersebut sama panjang.
“Jika dua sudut segitiga satu sama besar dengan dua sudut segitiga lainnya, dan sisi yang diapit oleh kedua sudut tersebut sama panjang, maka kedua segitiga tersebut kongruen.”
Misalnya, perhatikan segitiga ABC dan segitiga DEF di bawah ini:
Jika sudut A = sudut D, sudut B = sudut E, dan sisi AB = DE, maka segitiga ABC kongruen dengan segitiga DEF berdasarkan kriteria SAS.
Contoh Soal Kekongruenan Dua Segitiga
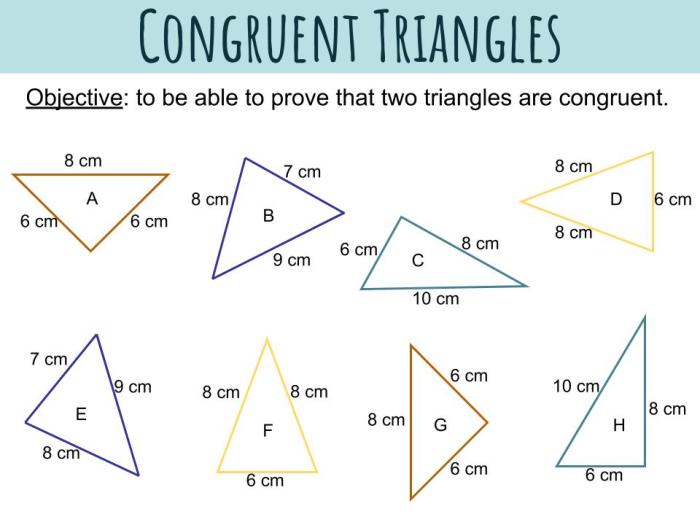
Kekongruenan dua segitiga merupakan konsep penting dalam geometri. Dua segitiga dikatakan kongruen jika ketiga sisi dan ketiga sudutnya memiliki ukuran yang sama. Ada beberapa kriteria yang dapat digunakan untuk menentukan apakah dua segitiga kongruen. Kriteria ini akan kita bahas melalui contoh soal berikut.
Contoh Soal Kekongruenan Dua Segitiga dengan Kriteria SSS
Kriteria SSS (Side-Side-Side) menyatakan bahwa dua segitiga kongruen jika ketiga sisi pada segitiga pertama sama panjang dengan ketiga sisi pada segitiga kedua. Perhatikan contoh soal berikut:
- Diketahui segitiga ABC dengan panjang sisi AB = 5 cm, BC = 7 cm, dan AC = 6 cm. Segitiga DEF memiliki panjang sisi DE = 5 cm, EF = 7 cm, dan DF = 6 cm. Tentukan apakah segitiga ABC dan DEF kongruen.
Penyelesaian:
- Perhatikan bahwa panjang sisi AB = DE = 5 cm, BC = EF = 7 cm, dan AC = DF = 6 cm. Artinya, ketiga sisi pada segitiga ABC sama panjang dengan ketiga sisi pada segitiga DEF.
- Berdasarkan kriteria SSS, karena ketiga sisi pada segitiga ABC sama panjang dengan ketiga sisi pada segitiga DEF, maka segitiga ABC dan DEF kongruen.
Contoh Soal Kekongruenan Dua Segitiga dengan Kriteria SAS
Kriteria SAS (Side-Angle-Side) menyatakan bahwa dua segitiga kongruen jika dua sisi dan sudut apit pada segitiga pertama sama dengan dua sisi dan sudut apit pada segitiga kedua. Perhatikan contoh soal berikut:
- Diketahui segitiga PQR dengan panjang sisi PQ = 8 cm, QR = 10 cm, dan sudut PQR = 60 derajat. Segitiga XYZ memiliki panjang sisi XY = 8 cm, YZ = 10 cm, dan sudut XYZ = 60 derajat. Tentukan apakah segitiga PQR dan XYZ kongruen.
Penyelesaian:
- Perhatikan bahwa panjang sisi PQ = XY = 8 cm, QR = YZ = 10 cm, dan sudut PQR = XYZ = 60 derajat. Artinya, dua sisi dan sudut apit pada segitiga PQR sama dengan dua sisi dan sudut apit pada segitiga XYZ.
- Berdasarkan kriteria SAS, karena dua sisi dan sudut apit pada segitiga PQR sama dengan dua sisi dan sudut apit pada segitiga XYZ, maka segitiga PQR dan XYZ kongruen.
Contoh Soal Kekongruenan Dua Segitiga dengan Kriteria ASA
Kriteria ASA (Angle-Side-Angle) menyatakan bahwa dua segitiga kongruen jika dua sudut dan sisi di antara kedua sudut tersebut pada segitiga pertama sama dengan dua sudut dan sisi di antara kedua sudut tersebut pada segitiga kedua. Perhatikan contoh soal berikut:
- Diketahui segitiga KLM dengan besar sudut K = 70 derajat, sudut L = 50 derajat, dan panjang sisi KL = 9 cm. Segitiga NOP memiliki besar sudut N = 70 derajat, sudut O = 50 derajat, dan panjang sisi NO = 9 cm. Tentukan apakah segitiga KLM dan NOP kongruen.
Penyelesaian:
- Perhatikan bahwa besar sudut K = N = 70 derajat, besar sudut L = O = 50 derajat, dan panjang sisi KL = NO = 9 cm. Artinya, dua sudut dan sisi di antara kedua sudut tersebut pada segitiga KLM sama dengan dua sudut dan sisi di antara kedua sudut tersebut pada segitiga NOP.
- Berdasarkan kriteria ASA, karena dua sudut dan sisi di antara kedua sudut tersebut pada segitiga KLM sama dengan dua sudut dan sisi di antara kedua sudut tersebut pada segitiga NOP, maka segitiga KLM dan NOP kongruen.
Contoh Soal Kekongruenan Dua Segitiga dengan Teorema Pythagoras
Teorema Pythagoras dapat digunakan untuk menentukan panjang sisi miring pada segitiga siku-siku. Jika diketahui panjang dua sisi pada segitiga siku-siku, maka panjang sisi miring dapat dihitung menggunakan teorema Pythagoras. Perhatikan contoh soal berikut:
- Diketahui segitiga ABC dengan sudut siku-siku di C. Panjang sisi AB = 10 cm dan BC = 6 cm. Segitiga DEF juga memiliki sudut siku-siku di F. Panjang sisi DE = 10 cm dan EF = 6 cm. Tentukan apakah segitiga ABC dan DEF kongruen.
Penyelesaian:
- Pertama, kita hitung panjang sisi AC menggunakan teorema Pythagoras:
- AC2 = AB2 – BC2 = 102 – 62 = 64
- AC = √64 = 8 cm
- Selanjutnya, kita hitung panjang sisi DF menggunakan teorema Pythagoras:
- DF2 = DE2 – EF2 = 102 – 62 = 64
- DF = √64 = 8 cm
- Perhatikan bahwa panjang sisi AB = DE = 10 cm, BC = EF = 6 cm, dan AC = DF = 8 cm. Artinya, ketiga sisi pada segitiga ABC sama panjang dengan ketiga sisi pada segitiga DEF.
- Berdasarkan kriteria SSS, karena ketiga sisi pada segitiga ABC sama panjang dengan ketiga sisi pada segitiga DEF, maka segitiga ABC dan DEF kongruen.
Penerapan Kekongruenan Segitiga
Konsep kekongruenan segitiga tidak hanya sebatas teori matematika, tetapi juga memiliki aplikasi nyata dalam berbagai bidang kehidupan. Pemahaman tentang kekongruenan segitiga memungkinkan kita untuk menyelesaikan berbagai masalah praktis, baik dalam bidang arsitektur, konstruksi, maupun geometri.
Penerapan Kekongruenan Segitiga dalam Arsitektur dan Konstruksi
Dalam dunia arsitektur dan konstruksi, kekongruenan segitiga berperan penting dalam memastikan kestabilan dan kekuatan bangunan. Salah satu contohnya adalah penggunaan rangka segitiga dalam konstruksi jembatan. Rangka segitiga yang kongruen memberikan kekuatan dan stabilitas yang optimal karena bentuknya yang kaku dan tidak mudah berubah bentuk. Hal ini karena, jika salah satu sisi segitiga mengalami tekanan, sisi lainnya akan menahan tekanan tersebut dan menjaga bentuk segitiga tetap utuh.
Penerapan Kekongruenan Segitiga dalam Geometri
Kekongruenan segitiga juga menjadi dasar dalam pembuktian teorema-teorema geometri. Dengan menggunakan konsep kekongruenan segitiga, kita dapat menunjukkan hubungan antar sisi dan sudut segitiga, serta membuktikan sifat-sifat bangun datar lainnya. Misalnya, teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat sisi lainnya, dapat dibuktikan dengan menggunakan konsep kekongruenan segitiga.
Contoh soal kekongruenan dua segitiga bisa dijumpai dalam berbagai buku pelajaran matematika. Misalnya, soal tentang membuktikan dua segitiga kongruen dengan menggunakan dalil sisi-sisi-sisi (SSS), sudut-sisi-sudut (SAS), atau sisi-sudut-sisi (SAS). Namun, jika kamu tertarik mempelajari dunia bisnis, kamu bisa menemukan contoh soal jurnal khusus perusahaan dagang beserta jawaban di sini.
Dengan memahami konsep kekongruenan, kamu bisa menyelesaikan berbagai masalah geometri, seperti menghitung luas dan keliling bangun datar. Begitu pula, dengan memahami jurnal khusus perusahaan dagang, kamu bisa mengelola keuangan perusahaan dengan lebih baik.
- Salah satu contohnya adalah pembuktian teorema Pythagoras. Teorema ini menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat sisi lainnya. Pembuktian ini melibatkan konstruksi segitiga kongruen yang membantu dalam memahami hubungan antar sisi segitiga.
- Konsep kekongruenan segitiga juga digunakan untuk membuktikan teorema tentang sudut-sudut dalam segitiga, seperti teorema tentang jumlah sudut dalam segitiga yang selalu 180 derajat. Pembuktian ini melibatkan konstruksi segitiga kongruen yang membantu dalam memahami hubungan antar sudut segitiga.
Contoh Penerapan Kekongruenan Segitiga dalam Kehidupan Sehari-hari
Penerapan konsep kekongruenan segitiga dalam kehidupan sehari-hari dapat kita temui dalam berbagai hal, misalnya:
- Pembuatan papan catur: Papan catur terdiri dari kotak-kotak persegi yang memiliki ukuran yang sama. Setiap kotak persegi dapat dibagi menjadi dua segitiga siku-siku yang kongruen. Dengan menggunakan konsep kekongruenan segitiga, kita dapat memastikan bahwa setiap kotak persegi memiliki ukuran yang sama, sehingga papan catur memiliki bentuk yang simetris.
- Pembuatan atap rumah: Atap rumah umumnya berbentuk segitiga. Untuk memastikan atap rumah memiliki bentuk yang simetris dan kokoh, diperlukan penggunaan konsep kekongruenan segitiga. Dengan memastikan bahwa setiap segitiga pada atap memiliki ukuran dan bentuk yang sama, maka atap rumah akan memiliki bentuk yang stabil dan kuat.
Soal Latihan Kekongruenan Segitiga
Setelah mempelajari tentang konsep kekongruenan dua segitiga, saatnya kita menguji pemahamanmu dengan mengerjakan soal latihan. Soal-soal berikut ini disusun dengan beragam tingkat kesulitan, mulai dari yang mudah hingga yang menantang. Mari kita selami dunia segitiga dan buktikan bahwa kamu mampu menguasai konsep kekongruenan!
Soal Latihan
Berikut adalah 5 soal latihan tentang kekongruenan dua segitiga yang dapat kamu kerjakan untuk mengasah kemampuanmu:
-
Diberikan dua segitiga ABC dan DEF. Diketahui bahwa ∠A = ∠D, ∠B = ∠E, dan AB = DE. Apakah kedua segitiga tersebut kongruen? Jika ya, sebutkan jenis kekongruenannya!
-
Segitiga PQR dan segitiga STU memiliki panjang sisi PQ = ST, QR = TU, dan PR = SU. Apakah kedua segitiga tersebut kongruen? Jika ya, sebutkan jenis kekongruenannya!
-
Segitiga KLM dan segitiga XYZ memiliki panjang sisi KL = XY, LM = YZ, dan ∠L = ∠Y. Apakah kedua segitiga tersebut kongruen? Jika ya, sebutkan jenis kekongruenannya!
-
Diberikan dua segitiga ABC dan DEF. Diketahui bahwa ∠A = ∠D, ∠B = ∠E, dan BC = EF. Apakah kedua segitiga tersebut kongruen? Jika ya, sebutkan jenis kekongruenannya!
-
Segitiga PQR dan segitiga STU memiliki panjang sisi PQ = ST, QR = TU, dan ∠Q = ∠T. Apakah kedua segitiga tersebut kongruen? Jika ya, sebutkan jenis kekongruenannya!
Kunci Jawaban
-
Ya, segitiga ABC dan DEF kongruen berdasarkan kriteria Sisi-Sudut-Sisi (SAS). Karena AB = DE, ∠A = ∠D, dan ∠B = ∠E, maka kedua segitiga tersebut kongruen.
-
Ya, segitiga PQR dan STU kongruen berdasarkan kriteria Sisi-Sisi-Sisi (SSS). Karena PQ = ST, QR = TU, dan PR = SU, maka kedua segitiga tersebut kongruen.
-
Ya, segitiga KLM dan XYZ kongruen berdasarkan kriteria Sisi-Sudut-Sisi (SAS). Karena KL = XY, LM = YZ, dan ∠L = ∠Y, maka kedua segitiga tersebut kongruen.
-
Ya, segitiga ABC dan DEF kongruen berdasarkan kriteria Sudut-Sisi-Sudut (ASA). Karena ∠A = ∠D, ∠B = ∠E, dan BC = EF, maka kedua segitiga tersebut kongruen.
-
Ya, segitiga PQR dan STU kongruen berdasarkan kriteria Sisi-Sudut-Sisi (SAS). Karena PQ = ST, QR = TU, dan ∠Q = ∠T, maka kedua segitiga tersebut kongruen.
Petunjuk Tambahan
Jika kamu kesulitan dalam menyelesaikan beberapa soal latihan, berikut adalah beberapa petunjuk tambahan yang mungkin dapat membantu:
-
Pastikan kamu memahami keempat kriteria kekongruenan segitiga, yaitu Sisi-Sisi-Sisi (SSS), Sisi-Sudut-Sisi (SAS), Sudut-Sisi-Sudut (ASA), dan Sudut-Sudut-Sisi (AAS).
-
Perhatikan dengan cermat informasi yang diberikan dalam soal. Identifikasi sisi-sisi dan sudut-sudut yang sama atau kongruen.
-
Jika kamu masih kesulitan, coba gambar kedua segitiga tersebut dan tandai sisi-sisi dan sudut-sudut yang sama atau kongruen. Hal ini akan membantu kamu untuk memvisualisasikan hubungan antara kedua segitiga tersebut.
Keunikan Kekongruenan Segitiga: Contoh Soal Kekongruenan Dua Segitiga
Konsep kekongruenan segitiga merupakan salah satu konsep fundamental dalam geometri. Dua segitiga dikatakan kongruen jika semua sisi dan sudutnya bersesuaian dan memiliki ukuran yang sama. Konsep ini sangat penting karena memungkinkan kita untuk membandingkan dan menganalisis bentuk dan ukuran segitiga, serta membuktikan teorema geometri lainnya.
Perbedaan Kekongruenan dan Kesebangunan
Konsep kekongruenan segitiga berbeda dengan konsep kesebangunan segitiga. Dua segitiga dikatakan sebangun jika sudut-sudutnya bersesuaian dan memiliki ukuran yang sama, tetapi sisi-sisinya tidak harus sama panjang. Dengan kata lain, segitiga sebangun memiliki bentuk yang sama tetapi ukuran yang berbeda, sedangkan segitiga kongruen memiliki bentuk dan ukuran yang sama.
- Kekongruenan: Sisi dan sudut bersesuaian sama.
- Kesebangunan: Sudut bersesuaian sama, sisi bersesuaian sebanding.
Membuktikan Teorema Geometri
Konsep kekongruenan segitiga dapat digunakan untuk membuktikan teorema geometri lainnya. Misalnya, teorema Pythagoras, yang menyatakan bahwa dalam segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat sisi lainnya, dapat dibuktikan dengan menggunakan konsep kekongruenan segitiga.
Memecahkan Masalah Geometri yang Lebih Kompleks
Konsep kekongruenan segitiga juga dapat digunakan untuk menyelesaikan masalah geometri yang lebih kompleks. Misalnya, dalam konstruksi, konsep kekongruenan segitiga dapat digunakan untuk memastikan bahwa dua bagian struktur memiliki ukuran dan bentuk yang sama. Konsep ini juga dapat digunakan dalam arsitektur, desain, dan berbagai bidang lainnya yang melibatkan pengukuran dan analisis bentuk geometri.
Contoh Soal Kekongruenan Segitiga dalam Bentuk Gambar
Untuk memahami konsep kekongruenan segitiga dengan lebih baik, mari kita lihat contoh soal yang menggunakan gambar. Soal ini akan menunjukkan bagaimana dua segitiga dapat dinyatakan kongruen berdasarkan sifat-sifat yang mereka miliki.
Contoh Soal Kekongruenan Segitiga
Perhatikan gambar dua segitiga berikut:
Gambarlah dua segitiga ABC dan DEF dengan sisi-sisi AB = DE, BC = EF, dan AC = DF.
Berdasarkan gambar tersebut, apakah segitiga ABC dan DEF kongruen? Jelaskan alasannya.
Langkah-langkah Penyelesaian
- Identifikasi Sisi yang Bersesuaian: Perhatikan sisi-sisi yang memiliki panjang yang sama pada kedua segitiga. Dalam contoh ini, AB = DE, BC = EF, dan AC = DF.
- Identifikasi Sudut yang Bersesuaian: Perhatikan sudut-sudut yang memiliki ukuran yang sama pada kedua segitiga. Karena sisi-sisi yang bersesuaian sama panjang, maka sudut-sudut yang bersesuaian juga akan sama besar. Misalnya, sudut A = sudut D, sudut B = sudut E, dan sudut C = sudut F.
- Terapkan Postulat Kekongruenan: Karena semua sisi dan sudut yang bersesuaian sama, maka segitiga ABC dan DEF kongruen berdasarkan postulat SSS (Side-Side-Side).
Kunci Jawaban
Ya, segitiga ABC dan DEF kongruen. Hal ini dapat dibuktikan dengan menggunakan postulat SSS (Side-Side-Side) karena ketiga sisi yang bersesuaian pada kedua segitiga memiliki panjang yang sama.
Perbedaan Kekongruenan dan Kesebangunan
Dalam geometri, kita seringkali menjumpai konsep kekongruenan dan kesebangunan pada bangun datar, khususnya segitiga. Meskipun keduanya membahas tentang kesamaan bentuk, terdapat perbedaan mendasar yang perlu dipahami. Perbedaan ini terletak pada ukuran dan bentuk dari bangun datar yang dibandingkan.
Perbedaan Kekongruenan dan Kesebangunan
Berikut tabel yang membandingkan dan membedakan konsep kekongruenan dan kesebangunan segitiga:
| Aspek | Kekongruenan | Kesebangunan |
|---|---|---|
| Definisi | Dua segitiga dikatakan kongruen jika memiliki bentuk dan ukuran yang sama. | Dua segitiga dikatakan sebangun jika memiliki bentuk yang sama, tetapi ukurannya tidak harus sama. |
| Syarat | – Sisi-Sisi-Sisi (SSS) – Sisi-Sudut-Sisi (SAS) – Sudut-Sisi-Sudut (ASA) – Sudut-Sudut-Sisi (SSA) |
– Sudut-Sudut-Sudut (AAA) – Sisi-Sisi-Sisi (SSS) – Sisi-Sudut-Sisi (SAS) |
| Hubungan Sisi | Semua sisi memiliki panjang yang sama. | Sisi-sisi yang bersesuaian memiliki perbandingan yang sama. |
| Hubungan Sudut | Semua sudut memiliki ukuran yang sama. | Semua sudut memiliki ukuran yang sama. |
| Contoh | Dua segitiga yang memiliki semua sisi dan sudut yang sama. | Dua segitiga yang memiliki bentuk yang sama, tetapi ukurannya berbeda, misalnya, segitiga kecil dan segitiga besar dengan bentuk yang sama. |
Contoh Ilustrasi
Untuk lebih memahami perbedaan antara kekongruenan dan kesebangunan, perhatikan contoh ilustrasi berikut:
Contoh 1: Dua segitiga yang kongruen
Misalnya, segitiga ABC dan segitiga DEF memiliki panjang sisi yang sama dan sudut yang sama. Kedua segitiga tersebut dapat saling ditumpuk sempurna sehingga terlihat bahwa mereka memiliki bentuk dan ukuran yang sama. Ini menunjukkan bahwa segitiga ABC dan segitiga DEF kongruen.
Contoh 2: Dua segitiga yang sebangun
Misalnya, segitiga PQR dan segitiga XYZ memiliki bentuk yang sama, tetapi ukurannya berbeda. Segitiga PQR lebih kecil daripada segitiga XYZ. Meskipun ukurannya berbeda, kedua segitiga memiliki perbandingan sisi yang sama dan sudut yang sama. Ini menunjukkan bahwa segitiga PQR dan segitiga XYZ sebangun.
Pembuktian Kekongruenan Segitiga
Dalam geometri, memahami konsep kekongruenan segitiga sangat penting. Dua segitiga dikatakan kongruen jika memiliki bentuk dan ukuran yang sama. Untuk membuktikan kekongruenan dua segitiga, kita dapat memanfaatkan beberapa kriteria atau postulat. Artikel ini akan membahas langkah-langkah yang dapat dilakukan untuk membuktikan kekongruenan dua segitiga, memberikan contoh soal, dan menjelaskan bagaimana konsep ini dapat diterapkan dalam menyelesaikan masalah geometri yang lebih kompleks.
Kriteria Kekongruenan Segitiga, Contoh soal kekongruenan dua segitiga
Ada lima kriteria utama yang dapat digunakan untuk membuktikan kekongruenan dua segitiga. Berikut penjelasan singkatnya:
- Sisi-Sisi-Sisi (SSS): Dua segitiga kongruen jika ketiga sisi pada segitiga pertama sama panjang dengan ketiga sisi pada segitiga kedua.
- Sisi-Sudut-Sisi (SAS): Dua segitiga kongruen jika dua sisi dan sudut apit pada segitiga pertama sama panjang dan besar dengan dua sisi dan sudut apit pada segitiga kedua.
- Sudut-Sisi-Sudut (ASA): Dua segitiga kongruen jika dua sudut dan sisi di antara kedua sudut tersebut pada segitiga pertama sama besar dan panjang dengan dua sudut dan sisi di antara kedua sudut tersebut pada segitiga kedua.
- Sudut-Sudut-Sisi (SSA): Kriteria ini tidak selalu menjamin kekongruenan. Ada kemungkinan dua segitiga memiliki dua sudut dan sisi yang sama panjang, namun tidak kongruen. Hal ini disebut dengan kasus ambigu.
- Sisi-Sudut-Sudut (SAA): Dua segitiga kongruen jika satu sisi dan dua sudut pada segitiga pertama sama panjang dan besar dengan satu sisi dan dua sudut pada segitiga kedua. Kriteria ini mirip dengan ASA, hanya saja posisi sudut dan sisi yang dibandingkan berbeda.
Contoh Soal dan Penyelesaian
Misalkan kita memiliki dua segitiga, yaitu segitiga ABC dan segitiga DEF. Diketahui bahwa AB = DE, BC = EF, dan AC = DF. Kita ingin membuktikan bahwa segitiga ABC kongruen dengan segitiga DEF.
Berdasarkan informasi yang diberikan, kita dapat menerapkan kriteria SSS. Karena ketiga sisi pada segitiga ABC sama panjang dengan ketiga sisi pada segitiga DEF, maka segitiga ABC kongruen dengan segitiga DEF. Simbol untuk menyatakan kekongruenan adalah ≅, sehingga dapat ditulis sebagai ΔABC ≅ ΔDEF.
Penerapan Kekongruenan Segitiga dalam Masalah Geometri
Konsep kekongruenan segitiga sangat bermanfaat dalam menyelesaikan berbagai masalah geometri, seperti:
- Menentukan panjang sisi atau besar sudut yang belum diketahui: Jika dua segitiga diketahui kongruen, maka semua sisi dan sudut yang bersesuaian pada kedua segitiga tersebut sama panjang dan besar.
- Membuktikan kesamaan bentuk dan ukuran bangun geometri: Kekongruenan segitiga dapat digunakan untuk membuktikan kesamaan bentuk dan ukuran bangun geometri yang lebih kompleks, seperti persegi panjang, persegi, atau trapesium.
- Menentukan hubungan antar garis dan sudut: Dengan menggunakan konsep kekongruenan segitiga, kita dapat menentukan hubungan antar garis dan sudut dalam suatu bangun geometri.
Penutupan
Dengan memahami konsep kekongruenan segitiga, kita dapat melihat keindahan geometri yang tersembunyi di sekitar kita. Dari arsitektur bangunan hingga desain pakaian, konsep ini berperan penting dalam menciptakan bentuk yang harmonis dan seimbang. Jadi, jangan ragu untuk menjelajahi lebih dalam dunia geometri dan mengungkap keajaiban yang tersembunyi di baliknya!






