Contoh soal nilai stasioner – Pernahkah Anda bertanya-tanya bagaimana menentukan titik tertinggi atau terendah dari sebuah grafik fungsi? Itulah yang dipelajari dalam konsep nilai stasioner. Dalam dunia matematika, nilai stasioner merupakan titik-titik penting pada grafik fungsi yang menunjukkan perubahan arah dari naik ke turun atau sebaliknya. Dengan memahami nilai stasioner, kita dapat menganalisis perilaku fungsi dan menyelesaikan berbagai masalah optimasi, seperti menentukan keuntungan maksimum atau biaya minimum dalam suatu bisnis.

Pada artikel ini, kita akan membahas secara detail tentang nilai stasioner, mulai dari definisi, cara menentukannya, jenis-jenisnya, hingga penerapannya dalam kehidupan nyata. Siap-siap untuk menjelajahi dunia nilai stasioner dan menguasai teknik menentukan titik-titik ekstrem dari fungsi!

Table of Contents:

Pengertian Nilai Stasioner

Dalam matematika, khususnya dalam kalkulus, nilai stasioner adalah titik pada kurva fungsi di mana turunan pertama fungsi tersebut sama dengan nol atau tidak terdefinisi. Pada titik-titik ini, kurva fungsi memiliki kemiringan nol atau tidak memiliki kemiringan. Nilai stasioner memainkan peran penting dalam memahami perilaku fungsi, seperti menentukan titik maksimum, minimum, dan titik belok.

Pengertian Nilai Stasioner dalam Konteks Fungsi

Nilai stasioner suatu fungsi adalah titik-titik pada kurva fungsi yang memiliki turunan pertama sama dengan nol atau tidak terdefinisi. Pada titik-titik ini, kurva fungsi memiliki kemiringan nol atau tidak memiliki kemiringan.

Contoh Fungsi dan Penentuan Nilai Stasionernya

Misalnya, perhatikan fungsi f(x) = x² – 4x + 3. Untuk menentukan nilai stasionernya, kita perlu menemukan turunan pertama fungsi tersebut, yaitu f'(x) = 2x – 4. Selanjutnya, kita cari titik-titik di mana f'(x) = 0. Dalam hal ini, f'(x) = 0 ketika x = 2. Jadi, x = 2 adalah nilai stasioner dari fungsi f(x) = x² – 4x + 3.

Langkah-Langkah Menentukan Nilai Stasioner dari Suatu Fungsi

Berikut adalah langkah-langkah untuk menentukan nilai stasioner dari suatu fungsi:

Tentukan turunan pertama fungsi tersebut.
Cari titik-titik di mana turunan pertama sama dengan nol atau tidak terdefinisi.
Titik-titik yang ditemukan pada langkah 2 adalah nilai stasioner dari fungsi tersebut.

Menentukan Nilai Stasioner

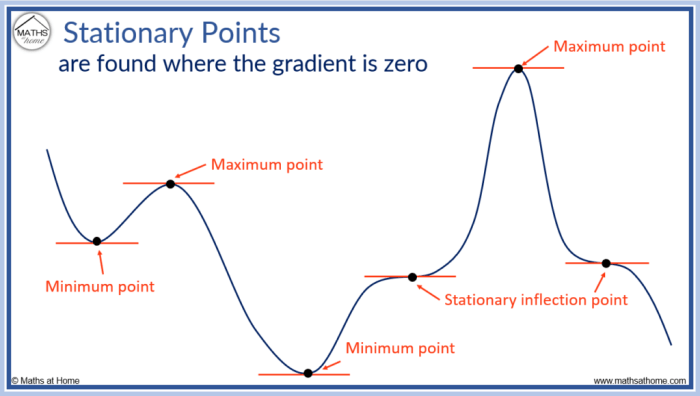
Nilai stasioner merupakan titik-titik pada kurva fungsi yang memiliki gradien nol. Pada titik-titik ini, fungsi mencapai titik puncak (maksimum) atau titik lembah (minimum), atau titik pelana (saddle point). Dalam menentukan nilai stasioner, turunan pertama fungsi memainkan peran penting.

Cara Menentukan Nilai Stasioner dengan Turunan Pertama

Berikut adalah cara menentukan nilai stasioner dari suatu fungsi dengan menggunakan turunan pertama:

Tentukan turunan pertama dari fungsi tersebut.
Cari nilai x yang membuat turunan pertama fungsi sama dengan nol (f'(x) = 0).
Tentukan titik-titik kritis (x) yang diperoleh dari langkah sebelumnya. Titik-titik kritis ini merupakan calon nilai stasioner.
Tentukan nilai y pada titik-titik kritis yang telah diperoleh.
Uji titik-titik kritis tersebut untuk menentukan apakah titik tersebut merupakan titik maksimum, minimum, atau titik pelana. Uji ini dapat dilakukan dengan menggunakan turunan kedua atau uji garis singgung.

Langkah-langkah Menentukan Nilai Stasioner

Langkah	Penjelasan
1. Tentukan turunan pertama fungsi.	Hitung turunan pertama dari fungsi f(x) dengan menggunakan aturan turunan yang sesuai.
2. Cari nilai x yang membuat turunan pertama fungsi sama dengan nol.	Selesaikan persamaan f'(x) = 0 untuk mencari nilai x.
3. Tentukan titik-titik kritis (x) yang diperoleh dari langkah sebelumnya.	Titik-titik kritis ini merupakan calon nilai stasioner.
4. Tentukan nilai y pada titik-titik kritis yang telah diperoleh.	Substitusikan nilai x yang telah diperoleh ke dalam fungsi f(x) untuk mendapatkan nilai y.
5. Uji titik-titik kritis tersebut untuk menentukan apakah titik tersebut merupakan titik maksimum, minimum, atau titik pelana.	Uji ini dapat dilakukan dengan menggunakan turunan kedua atau uji garis singgung.

Contoh Soal dan Solusi

Misalkan kita ingin menentukan nilai stasioner dari fungsi f(x) = x^3 – 3x^2 + 2x.

Tentukan turunan pertama dari fungsi tersebut:

f'(x) = 3x^2 – 6x + 2
Cari nilai x yang membuat turunan pertama fungsi sama dengan nol:

3x^2 – 6x + 2 = 0

x = (6 ± √(6^2 – 4 * 3 * 2)) / (2 * 3)

x = (6 ± √12) / 6

x = (6 ± 2√3) / 6

x = 1 ± √3 / 3

Jadi, nilai x yang membuat f'(x) = 0 adalah x = 1 + √3 / 3 dan x = 1 – √3 / 3.
Tentukan titik-titik kritis (x) yang diperoleh dari langkah sebelumnya:

x = 1 + √3 / 3 dan x = 1 – √3 / 3
Tentukan nilai y pada titik-titik kritis yang telah diperoleh:

Untuk x = 1 + √3 / 3, y = (1 + √3 / 3)^3 – 3(1 + √3 / 3)^2 + 2(1 + √3 / 3)

Untuk x = 1 – √3 / 3, y = (1 – √3 / 3)^3 – 3(1 – √3 / 3)^2 + 2(1 – √3 / 3)
Uji titik-titik kritis tersebut untuk menentukan apakah titik tersebut merupakan titik maksimum, minimum, atau titik pelana:

Untuk menentukan jenis titik kritis, kita dapat menggunakan turunan kedua:

f”(x) = 6x – 6

Untuk x = 1 + √3 / 3, f”(x) = 6(1 + √3 / 3) – 6 = 2√3 > 0. Karena f”(x) > 0, maka titik (1 + √3 / 3, f(1 + √3 / 3)) merupakan titik minimum.

Untuk x = 1 – √3 / 3, f”(x) = 6(1 – √3 / 3) – 6 = -2√3 < 0. Karena f''(x) < 0, maka titik (1 – √3 / 3, f(1 – √3 / 3)) merupakan titik maksimum.

Jenis-Jenis Nilai Stasioner

Setelah menemukan titik stasioner, langkah selanjutnya adalah menentukan jenis nilai stasioner tersebut. Ada tiga jenis nilai stasioner, yaitu titik maksimum, titik minimum, dan titik pelana. Ketiga jenis ini memiliki ciri-ciri yang berbeda dan dapat dibedakan berdasarkan turunan pertama dan kedua fungsi.

Titik Maksimum

Titik maksimum adalah titik di mana fungsi mencapai nilai tertinggi di sekitar titik tersebut. Dengan kata lain, nilai fungsi di titik maksimum lebih besar daripada nilai fungsi di titik-titik di sekitarnya.

Ciri-ciri titik maksimum:
- Turunan pertama fungsi bernilai nol di titik maksimum.
- Turunan kedua fungsi bernilai negatif di titik maksimum.
Contoh fungsi:
Misalkan fungsi f(x) = -x^2 + 4x – 3. Titik stasioner fungsi ini adalah x = 2. Turunan pertama fungsi adalah f'(x) = -2x + 4, dan turunan kedua fungsi adalah f”(x) = -2. Karena turunan kedua fungsi bernilai negatif di titik x = 2, maka titik x = 2 adalah titik maksimum fungsi f(x).

Titik Minimum

Titik minimum adalah titik di mana fungsi mencapai nilai terendah di sekitar titik tersebut. Dengan kata lain, nilai fungsi di titik minimum lebih kecil daripada nilai fungsi di titik-titik di sekitarnya.

Ciri-ciri titik minimum:
- Turunan pertama fungsi bernilai nol di titik minimum.
- Turunan kedua fungsi bernilai positif di titik minimum.
Contoh fungsi:
Misalkan fungsi g(x) = x^2 – 4x + 3. Titik stasioner fungsi ini adalah x = 2. Turunan pertama fungsi adalah g'(x) = 2x – 4, dan turunan kedua fungsi adalah g”(x) = 2. Karena turunan kedua fungsi bernilai positif di titik x = 2, maka titik x = 2 adalah titik minimum fungsi g(x).

Titik Pelana, Contoh soal nilai stasioner

Titik pelana adalah titik di mana fungsi tidak mencapai nilai maksimum atau minimum di sekitar titik tersebut. Dengan kata lain, nilai fungsi di titik pelana tidak lebih besar atau lebih kecil daripada nilai fungsi di titik-titik di sekitarnya.

Ciri-ciri titik pelana:
- Turunan pertama fungsi bernilai nol di titik pelana.
- Turunan kedua fungsi bernilai nol di titik pelana.
Contoh fungsi:
Misalkan fungsi h(x) = x^3. Titik stasioner fungsi ini adalah x = 0. Turunan pertama fungsi adalah h'(x) = 3x^2, dan turunan kedua fungsi adalah h”(x) = 6x. Karena turunan kedua fungsi bernilai nol di titik x = 0, maka titik x = 0 adalah titik pelana fungsi h(x).

Penerapan Nilai Stasioner: Contoh Soal Nilai Stasioner

Nilai stasioner, yang merupakan titik-titik pada grafik fungsi di mana turunannya sama dengan nol atau tidak terdefinisi, memiliki peran penting dalam berbagai bidang, terutama dalam masalah optimasi. Penerapan nilai stasioner memungkinkan kita untuk menentukan titik-titik ekstrem, yaitu titik maksimum atau minimum dari suatu fungsi, yang sangat berguna dalam menentukan nilai optimal dalam berbagai situasi.

Penerapan Nilai Stasioner dalam Masalah Optimasi

Dalam masalah optimasi, kita sering kali ingin menemukan nilai maksimum atau minimum dari suatu fungsi. Nilai stasioner memberikan kita alat untuk menentukan titik-titik ekstrem yang mungkin dari fungsi tersebut. Titik-titik ekstrem ini kemudian dapat dianalisis lebih lanjut untuk menentukan nilai maksimum atau minimum yang sebenarnya.

Contoh Soal Penerapan Nilai Stasioner

Misalnya, kita ingin menentukan nilai maksimum dari fungsi f(x) = -x² + 4x + 5. Berikut langkah-langkahnya:

Tentukan turunan pertama dari fungsi f(x).
f'(x) = -2x + 4
Cari nilai x yang membuat turunan pertama sama dengan nol.
f'(x) = -2x + 4 = 0

x = 2

Mencari nilai stasioner pada fungsi memang menantang, ya? Tapi tenang, latihan soal bisa bantu kamu menguasainya! Contohnya, cari nilai stasioner dari fungsi f(x) = x^3 – 3x^2 + 2x. Nah, kalau kamu ingin belajar soal perpajakan, coba deh cek contoh soal PPh badan dan jawabannya.

Soal PPh badan bisa jadi latihan yang seru untuk mengasah kemampuan analitis kamu, lho! Setelahnya, kamu bisa kembali berlatih soal nilai stasioner dengan lebih percaya diri.
Tentukan nilai f(x) pada nilai x yang diperoleh.
f(2) = -(2)² + 4(2) + 5 = 9

Dengan demikian, nilai maksimum dari fungsi f(x) = -x² + 4x + 5 adalah 9, yang dicapai pada x = 2.

Langkah-Langkah Menyelesaikan Masalah Optimasi dengan Nilai Stasioner

Berikut adalah langkah-langkah umum untuk menyelesaikan masalah optimasi dengan nilai stasioner:

Tentukan fungsi yang ingin dioptimalkan (dimaksimumkan atau diminimumkan).
Tentukan domain fungsi, yaitu rentang nilai x yang diperbolehkan.
Tentukan turunan pertama dari fungsi tersebut.
Cari nilai x yang membuat turunan pertama sama dengan nol atau tidak terdefinisi. Ini adalah nilai-nilai stasioner.
Tentukan nilai fungsi pada nilai-nilai stasioner dan pada ujung domain fungsi.
Bandingkan nilai-nilai fungsi yang diperoleh untuk menentukan nilai maksimum atau minimum yang sebenarnya.

Soal Latihan

Setelah mempelajari konsep nilai stasioner, mari kita uji pemahamanmu dengan beberapa soal latihan. Soal-soal ini dirancang dengan tingkat kesulitan yang bervariasi, mulai dari yang mudah hingga yang menantang. Selesaikan soal-soal ini dengan langkah-langkah yang sistematis dan cermat untuk mengasah kemampuanmu dalam menentukan nilai stasioner fungsi.

Soal Latihan Nilai Stasioner

Berikut adalah 5 soal latihan tentang nilai stasioner yang dapat kamu kerjakan untuk menguji pemahamanmu:

Soal	Solusi	Pembahasan
Tentukan nilai stasioner dari fungsi f(x) = x² – 4x + 3.	1. Cari turunan pertama fungsi f(x): f'(x) = 2x – 4 2. Temukan titik-titik kritis dengan menyelesaikan persamaan f'(x) = 0: 2x – 4 = 0 x = 2 3. Hitung nilai fungsi f(x) di titik kritis x = 2: f(2) = 2² – 4(2) + 3 = -1 Jadi, nilai stasioner dari fungsi f(x) = x² – 4x + 3 adalah -1.	Nilai stasioner terjadi ketika turunan pertama fungsi sama dengan nol. Titik kritis x = 2 merupakan titik stasioner, dan nilai fungsi f(x) di titik tersebut adalah nilai stasionernya.
Tentukan nilai stasioner dari fungsi f(x) = x³ – 3x² + 2.	1. Cari turunan pertama fungsi f(x): f'(x) = 3x² – 6x 2. Temukan titik-titik kritis dengan menyelesaikan persamaan f'(x) = 0: 3x² – 6x = 0 3x(x – 2) = 0 x = 0 atau x = 2 3. Hitung nilai fungsi f(x) di titik kritis x = 0 dan x = 2: f(0) = 0³ – 3(0)² + 2 = 2 f(2) = 2³ – 3(2)² + 2 = -2 Jadi, nilai stasioner dari fungsi f(x) = x³ – 3x² + 2 adalah 2 dan -2.	Fungsi ini memiliki dua titik kritis, sehingga terdapat dua nilai stasioner.
Tentukan nilai stasioner dari fungsi f(x) = 2x⁴ – 8x² + 5.	1. Cari turunan pertama fungsi f(x): f'(x) = 8x³ – 16x 2. Temukan titik-titik kritis dengan menyelesaikan persamaan f'(x) = 0: 8x³ – 16x = 0 8x(x² – 2) = 0 x = 0 atau x = √2 atau x = -√2 3. Hitung nilai fungsi f(x) di titik kritis x = 0, x = √2, dan x = -√2: f(0) = 2(0)⁴ – 8(0)² + 5 = 5 f(√2) = 2(√2)⁴ – 8(√2)² + 5 = -3 f(-√2) = 2(-√2)⁴ – 8(-√2)² + 5 = -3 Jadi, nilai stasioner dari fungsi f(x) = 2x⁴ – 8x² + 5 adalah 5, -3, dan -3.	Fungsi ini memiliki tiga titik kritis, sehingga terdapat tiga nilai stasioner.
Tentukan nilai stasioner dari fungsi f(x) = sin(x) pada interval 0 ≤ x ≤ 2π.	1. Cari turunan pertama fungsi f(x): f'(x) = cos(x) 2. Temukan titik-titik kritis dengan menyelesaikan persamaan f'(x) = 0: cos(x) = 0 x = π/2 atau x = 3π/2 3. Hitung nilai fungsi f(x) di titik kritis x = π/2 dan x = 3π/2: f(π/2) = sin(π/2) = 1 f(3π/2) = sin(3π/2) = -1 Jadi, nilai stasioner dari fungsi f(x) = sin(x) pada interval 0 ≤ x ≤ 2π adalah 1 dan -1.	Fungsi trigonometri memiliki nilai stasioner pada titik-titik di mana turunan pertamanya sama dengan nol.
Tentukan nilai stasioner dari fungsi f(x) = e^x + e^-x.	1. Cari turunan pertama fungsi f(x): f'(x) = e^x – e^-x 2. Temukan titik-titik kritis dengan menyelesaikan persamaan f'(x) = 0: e^x – e^-x = 0 e^x = e^-x x = 0 3. Hitung nilai fungsi f(x) di titik kritis x = 0: f(0) = e⁰ + e^-0 = 2 Jadi, nilai stasioner dari fungsi f(x) = e^x + e^-x adalah 2.	Fungsi eksponensial juga memiliki nilai stasioner, yang dapat ditentukan dengan mencari titik kritis di mana turunan pertamanya sama dengan nol.

Ilustrasi Grafik

Memahami nilai stasioner tidak hanya sebatas perhitungan matematika. Visualisasi melalui grafik fungsi memberikan pemahaman yang lebih mendalam tentang bagaimana nilai stasioner bermanifestasi pada bentuk kurva. Dengan mengamati grafik, kita dapat dengan mudah mengenali titik-titik stasioner dan menghubungkannya dengan jenis nilai stasioner yang diwakili.

Memvisualisasikan Nilai Stasioner

Bayangkan sebuah grafik fungsi yang menunjukkan hubungan antara variabel input dan output. Titik stasioner pada grafik ini merupakan titik-titik di mana garis singgung pada kurva memiliki kemiringan nol. Dengan kata lain, di titik-titik ini, kurva tidak naik atau turun, tetapi “stasioner” atau datar.

Jika kurva memiliki titik minimum, maka titik tersebut adalah titik stasioner dengan nilai stasioner minimum.
Jika kurva memiliki titik maksimum, maka titik tersebut adalah titik stasioner dengan nilai stasioner maksimum.
Jika kurva memiliki titik belok, maka titik tersebut adalah titik stasioner dengan nilai stasioner yang bukan maksimum atau minimum.

Contoh Ilustrasi

Misalnya, perhatikan grafik fungsi kuadrat y = x² – 2x + 1. Grafik fungsi ini berbentuk parabola yang membuka ke atas. Titik minimum pada parabola ini merupakan titik stasioner, di mana garis singgung pada kurva memiliki kemiringan nol. Titik ini juga merupakan titik balik, karena kurva berubah dari turun ke naik di titik ini.

Titik stasioner pada grafik ini dapat diidentifikasi dengan mencari titik di mana turunan pertama fungsi sama dengan nol. Turunan pertama dari fungsi y = x² – 2x + 1 adalah y’ = 2x – 2. Dengan menyelesaikan persamaan y’ = 0, kita memperoleh x = 1. Jadi, titik stasioner pada grafik fungsi ini adalah (1, 0).

Hubungan Antara Jenis Nilai Stasioner dengan Bentuk Grafik Fungsi

Hubungan antara jenis nilai stasioner dengan bentuk grafik fungsi dapat dijelaskan sebagai berikut:

Titik Minimum: Jika turunan pertama fungsi bernilai negatif sebelum titik stasioner dan bernilai positif setelah titik stasioner, maka titik stasioner tersebut adalah titik minimum. Grafik fungsi akan berbentuk cekung ke atas di sekitar titik minimum.
Titik Maksimum: Jika turunan pertama fungsi bernilai positif sebelum titik stasioner dan bernilai negatif setelah titik stasioner, maka titik stasioner tersebut adalah titik maksimum. Grafik fungsi akan berbentuk cekung ke bawah di sekitar titik maksimum.
Titik Belok: Jika turunan pertama fungsi tidak berubah tanda sebelum dan setelah titik stasioner, maka titik stasioner tersebut adalah titik belok. Grafik fungsi tidak berubah bentuk cekung di sekitar titik belok, tetapi hanya memiliki garis singgung yang horizontal.

Aplikasi dalam Kehidupan Nyata

Nilai stasioner tidak hanya konsep abstrak dalam matematika. Konsep ini memiliki aplikasi yang luas dalam berbagai bidang kehidupan nyata. Nilai stasioner membantu kita memahami dan memecahkan masalah praktis yang kita hadapi sehari-hari, dari menentukan titik optimal dalam produksi hingga merancang struktur yang efisien.

Contoh Aplikasi Nilai Stasioner dalam Kehidupan Nyata

Berikut adalah beberapa contoh aplikasi nilai stasioner dalam kehidupan nyata:

Optimasi Produksi: Dalam industri manufaktur, nilai stasioner digunakan untuk menentukan jumlah produk yang optimal yang harus diproduksi untuk memaksimalkan keuntungan. Misalnya, perusahaan dapat menggunakan kalkulus untuk menemukan titik produksi di mana biaya produksi minimal dan keuntungan maksimal.
Desain Struktur: Arsitek dan insinyur menggunakan nilai stasioner untuk merancang struktur yang kuat dan efisien. Mereka dapat menentukan bentuk dan ukuran yang optimal untuk jembatan, gedung, dan struktur lainnya dengan mempertimbangkan kekuatan material dan beban yang akan ditanggung.
Analisis Ekonomi: Nilai stasioner juga diterapkan dalam ekonomi untuk menganalisis pertumbuhan ekonomi, tingkat inflasi, dan perilaku konsumen. Contohnya, ekonom dapat menggunakan nilai stasioner untuk memodelkan hubungan antara tingkat suku bunga dan tingkat investasi.
Pengolahan Citra: Dalam pengolahan citra, nilai stasioner digunakan untuk menemukan tepi dan fitur penting dalam gambar. Algoritma pengolahan citra menggunakan konsep nilai stasioner untuk mengidentifikasi perubahan tajam dalam intensitas cahaya, yang membantu dalam mendeteksi objek dan tepi dalam gambar.

Cara Penerapan Nilai Stasioner dalam Masalah Praktis

Untuk menerapkan nilai stasioner dalam menyelesaikan masalah praktis, langkah-langkah berikut dapat digunakan:

Membangun Model Matematika: Langkah pertama adalah membangun model matematika yang mewakili masalah yang ingin dipecahkan. Model ini biasanya berupa fungsi yang menggambarkan hubungan antara variabel-variabel yang terlibat dalam masalah.
Mencari Nilai Stasioner: Setelah model matematika dibangun, langkah selanjutnya adalah mencari nilai stasioner dari fungsi tersebut. Nilai stasioner adalah titik-titik di mana turunan pertama fungsi sama dengan nol atau tidak terdefinisi.
Menganalisis Nilai Stasioner: Setelah menemukan nilai stasioner, langkah selanjutnya adalah menganalisis nilai stasioner tersebut untuk menentukan apakah mereka merupakan titik minimum, maksimum, atau titik pelana. Analisis ini biasanya dilakukan dengan menggunakan turunan kedua fungsi.
Interpretasi Hasil: Langkah terakhir adalah menginterpretasikan hasil analisis dalam konteks masalah yang ingin dipecahkan. Hasil ini dapat digunakan untuk membuat keputusan dan mengambil tindakan yang optimal dalam menyelesaikan masalah.

Penutupan

Memahami nilai stasioner membuka pintu bagi kita untuk menguasai teknik analisis fungsi yang lebih mendalam. Dengan kemampuan menentukan titik-titik ekstrem, kita dapat memecahkan berbagai masalah optimasi, baik dalam bidang matematika maupun dalam kehidupan nyata. Jadi, jangan ragu untuk memperdalam pemahaman Anda tentang nilai stasioner dan gunakannya untuk menyelesaikan berbagai tantangan yang Anda hadapi.