Matematika Teknik Sipil, seperti tulang punggung yang kokoh, menjadi pondasi bagi setiap bangunan megah yang menjulang tinggi. Bayangkan, sebuah jembatan yang membentang melintasi sungai, gedung pencakar langit yang menyapa langit, atau bendungan yang menahan derasnya air. Di balik keindahan dan kemegahannya, tersembunyi rumus-rumus matematika yang rumit, perhitungan presisi, dan simulasi yang cermat. Tanpa matematika, mimpi-mimpi arsitektur hanya akan menjadi bayangan kosong.
Matematika bukan hanya sekadar angka dan rumus, melainkan alat yang ampuh untuk merancang, membangun, dan memelihara struktur yang aman dan tahan lama. Dari perencanaan hingga konstruksi, setiap tahap pembangunan melibatkan aplikasi matematika yang kompleks. Mulai dari kalkulus yang membantu menganalisis tegangan dan deformasi struktur, aljabar linear untuk memodelkan perilaku material, hingga geometri dan trigonometri untuk mengukur dan memetakan lokasi konstruksi.
Pentingnya Matematika dalam Teknik Sipil
Teknik sipil adalah bidang yang luas yang melibatkan perencanaan, desain, konstruksi, dan pemeliharaan infrastruktur seperti bangunan, jembatan, jalan, dan bendungan. Bidang ini membutuhkan pemahaman yang mendalam tentang prinsip-prinsip ilmiah dan matematika, yang merupakan dasar fundamental untuk memecahkan masalah teknik dan membuat keputusan yang tepat.
Matematika memainkan peran penting dalam berbagai aspek teknik sipil, dari perhitungan beban dan kekuatan struktur hingga perencanaan aliran air dan desain sistem drainase. Tanpa matematika, para insinyur sipil tidak akan dapat membangun struktur yang aman, efisien, dan tahan lama.
Aplikasi Matematika dalam Teknik Sipil
Berikut ini adalah beberapa contoh konkret bagaimana matematika diterapkan dalam teknik sipil:
- Perencanaan dan Desain Bangunan: Matematika digunakan untuk menghitung beban yang akan ditanggung oleh struktur, menentukan ukuran dan bentuk elemen struktur, dan memastikan stabilitas bangunan. Contohnya, dalam desain jembatan, matematika digunakan untuk menghitung gaya tarik dan tekan yang terjadi pada struktur jembatan akibat beban kendaraan dan angin.
- Geoteknik: Matematika digunakan untuk menganalisis sifat tanah dan batuan, seperti kekuatan geser dan daya dukung, yang penting untuk desain pondasi bangunan dan struktur bawah tanah. Misalnya, dalam desain pondasi, matematika digunakan untuk menghitung kedalaman dan ukuran pondasi yang diperlukan untuk menopang beban bangunan.
- Hidrolika: Matematika digunakan untuk menganalisis aliran air dan pergerakan fluida, yang penting untuk desain sistem drainase, saluran air, dan bendungan. Contohnya, dalam desain sistem drainase, matematika digunakan untuk menghitung volume air hujan yang harus ditampung oleh sistem drainase dan menentukan ukuran saluran air yang diperlukan.
Perbandingan Aplikasi Matematika dalam Bidang Teknik Sipil, Matematika teknik sipil
| Bidang Teknik Sipil | Aplikasi Matematika |
|---|---|
| Struktur | Kalkulus, aljabar linear, persamaan diferensial, geometri, trigonometri |
| Geoteknik | Kalkulus, mekanika tanah, statistik, probabilitas |
| Hidrolika | Kalkulus, mekanika fluida, persamaan diferensial, statistik |
Cabang Matematika yang Digunakan dalam Teknik Sipil: Matematika Teknik Sipil
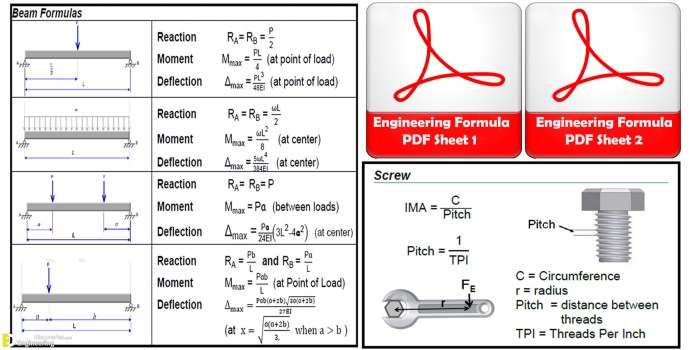
Teknik sipil, sebagai bidang yang berfokus pada desain, konstruksi, dan pemeliharaan infrastruktur, sangat bergantung pada prinsip-prinsip matematika. Matematika memberikan kerangka kerja yang kuat untuk menyelesaikan masalah teknik yang kompleks, memungkinkan insinyur untuk merancang struktur yang aman, efisien, dan tahan lama.
Kalkulus
Kalkulus adalah salah satu cabang matematika yang paling penting dalam teknik sipil. Kalkulus memungkinkan insinyur untuk menganalisis perubahan dan gerakan, yang sangat penting dalam memahami perilaku struktur di bawah beban. Kalkulus digunakan untuk:
- Analisis Struktur: Kalkulus digunakan untuk menentukan tegangan dan regangan dalam struktur, seperti jembatan dan gedung, di bawah berbagai beban. Ini membantu insinyur untuk merancang struktur yang dapat menahan beban yang diharapkan tanpa gagal.
- Perhitungan Beban: Kalkulus membantu dalam menghitung beban yang bekerja pada struktur, seperti beban angin, beban gempa bumi, dan beban mati (berat struktur itu sendiri). Dengan memahami beban-beban ini, insinyur dapat merancang struktur yang dapat menahannya dengan aman.
Aljabar Linear
Aljabar linear, yang mempelajari vektor, matriks, dan sistem persamaan linear, merupakan alat penting dalam pemodelan dan simulasi struktur. Aljabar linear digunakan untuk:
- Pemodelan Struktur: Aljabar linear memungkinkan insinyur untuk merepresentasikan struktur sebagai sistem persamaan linear, yang dapat dipecahkan untuk menentukan perilaku struktur di bawah beban. Ini membantu dalam desain dan analisis struktur yang kompleks.
- Simulasi Struktur: Aljabar linear digunakan untuk mengembangkan model komputer yang mensimulasikan perilaku struktur di bawah berbagai kondisi. Ini memungkinkan insinyur untuk mengevaluasi desain dan mengidentifikasi potensi masalah sebelum konstruksi dimulai.
Geometri dan Trigonometri
Geometri dan trigonometri, yang mempelajari bentuk, ukuran, dan posisi objek, sangat penting dalam pengukuran dan pemetaan. Kedua cabang matematika ini digunakan untuk:
- Pengukuran Tanah: Geometri dan trigonometri digunakan untuk menentukan ukuran dan bentuk lahan, yang penting dalam perencanaan dan konstruksi proyek infrastruktur.
- Pemetaan: Geometri dan trigonometri digunakan untuk membuat peta dan rencana situs konstruksi. Ini memungkinkan insinyur untuk merencanakan konstruksi secara akurat dan menghindari kesalahan.
Aplikasi Matematika dalam Perencanaan dan Desain Struktur

Matematika merupakan dasar fundamental dalam bidang teknik sipil, khususnya dalam perencanaan dan desain struktur. Aplikasi matematika memungkinkan para insinyur untuk menganalisis perilaku struktur, menentukan kekuatan dan stabilitasnya, serta memastikan keamanan dan ketahanan terhadap beban yang ditimbulkan.
Persamaan Diferensial dalam Analisis Struktur
Persamaan diferensial memainkan peran penting dalam analisis struktur, khususnya dalam menentukan tegangan dan deformasi pada struktur. Persamaan diferensial membantu dalam memahami bagaimana beban yang diterapkan pada struktur memengaruhi distribusi tegangan dan deformasi pada berbagai bagian struktur.
Contohnya, persamaan diferensial digunakan untuk menganalisis perilaku balok yang dibebani, menentukan bagaimana beban terdistribusi di sepanjang balok, dan bagaimana balok akan melengkung (deformasi) sebagai respons terhadap beban tersebut.
Aplikasi Matematika dalam Desain Struktur
Matematika digunakan secara luas dalam desain berbagai jenis struktur, seperti jembatan, gedung tinggi, dan bendungan. Aplikasi matematika memungkinkan para insinyur untuk menentukan dimensi, material, dan konfigurasi struktur yang optimal untuk memastikan kekuatan, stabilitas, dan keamanan.
- Desain Jembatan: Matematika digunakan untuk menentukan bentuk, ukuran, dan material jembatan yang optimal, mempertimbangkan beban yang akan ditanggung, seperti lalu lintas, angin, dan gempa bumi. Persamaan matematika digunakan untuk menghitung kekuatan dan stabilitas jembatan, memastikan bahwa jembatan dapat menahan beban tanpa runtuh.
- Desain Gedung Tinggi: Matematika digunakan untuk menghitung beban angin, gempa bumi, dan beban lainnya yang bekerja pada gedung tinggi. Persamaan matematika juga digunakan untuk menentukan ukuran dan konfigurasi kolom, balok, dan struktur penahan beban lainnya, memastikan bahwa gedung dapat menahan beban tanpa mengalami deformasi yang berlebihan atau runtuh.
- Desain Bendungan: Matematika digunakan untuk menghitung tekanan air yang bekerja pada bendungan, serta untuk menentukan bentuk, ukuran, dan material bendungan yang optimal. Persamaan matematika juga digunakan untuk menganalisis stabilitas bendungan, memastikan bahwa bendungan dapat menahan tekanan air dan tidak runtuh.
Ilustrasi Penerapan Persamaan Matematika dalam Perhitungan Beban dan Kekuatan
Sebagai ilustrasi sederhana, perhatikan sebuah balok sederhana yang dibebani di tengahnya. Beban yang bekerja pada balok menyebabkan balok melengkung (deformasi). Persamaan matematika dapat digunakan untuk menentukan besarnya deformasi dan tegangan yang terjadi pada balok.
Misalnya, persamaan lenturan balok dapat digunakan untuk menghitung momen lentur yang terjadi pada balok. Momen lentur merupakan ukuran gaya rotasi yang bekerja pada balok dan dapat digunakan untuk menentukan tegangan yang terjadi pada balok. Dengan menggunakan persamaan matematika, para insinyur dapat menentukan apakah balok cukup kuat untuk menahan beban yang diberikan tanpa mengalami deformasi yang berlebihan atau runtuh.
Persamaan matematika lainnya, seperti persamaan keseimbangan gaya dan momen, juga dapat digunakan untuk menganalisis perilaku balok dan struktur lainnya. Dengan menggunakan persamaan matematika ini, para insinyur dapat memastikan bahwa struktur dirancang dengan aman dan dapat menahan beban yang diberikan tanpa mengalami deformasi yang berlebihan atau runtuh.
Peran Matematika dalam Analisis dan Simulasi

Matematika berperan penting dalam analisis dan simulasi struktur dalam teknik sipil. Metode numerik dan pemodelan komputer memungkinkan insinyur untuk menganalisis perilaku struktur di bawah berbagai kondisi beban. Dengan menggunakan matematika, insinyur dapat memprediksi kekuatan, stabilitas, dan perilaku struktur sebelum konstruksi, sehingga dapat meminimalkan risiko kegagalan dan memastikan keamanan struktur.
Metode Numerik dan Pemodelan Komputer dalam Analisis Struktur
Metode numerik adalah teknik matematika yang digunakan untuk menyelesaikan persamaan diferensial yang kompleks yang menggambarkan perilaku struktur. Teknik ini melibatkan pembagian struktur menjadi elemen-elemen kecil, yang kemudian dianalisis secara individual. Dengan menggunakan metode numerik, insinyur dapat menghitung gaya internal, tegangan, dan perpindahan pada setiap elemen, dan kemudian menggabungkan hasil tersebut untuk memperoleh gambaran keseluruhan perilaku struktur.
Pemodelan komputer menggunakan perangkat lunak khusus untuk menciptakan representasi digital dari struktur yang akan dianalisis. Model ini dapat mencakup geometri, bahan, dan kondisi beban yang kompleks. Dengan menggunakan pemodelan komputer, insinyur dapat melakukan simulasi perilaku struktur di bawah berbagai kondisi, seperti gempa bumi, angin kencang, atau beban statis. Hasil simulasi ini dapat digunakan untuk mengevaluasi kekuatan, stabilitas, dan perilaku struktur, dan untuk mengidentifikasi potensi masalah sebelum konstruksi.
Simulasi Perilaku Struktur dengan Matematika
Matematika memungkinkan insinyur untuk mensimulasikan perilaku struktur di bawah berbagai kondisi beban, seperti beban statis, beban dinamis, dan beban termal. Simulasi ini membantu insinyur dalam memprediksi:
- Kekuatan struktur: Kemampuan struktur untuk menahan beban tanpa mengalami kegagalan.
- Stabilitas struktur: Kemampuan struktur untuk mempertahankan keseimbangan dan tidak runtuh.
- Perpindahan struktur: Perubahan bentuk struktur di bawah beban.
- Tegangan dan regangan: Gaya internal yang bekerja pada struktur.
- Frekuensi alami struktur: Kecenderungan struktur untuk bergetar pada frekuensi tertentu.
Simulasi ini dapat digunakan untuk mengevaluasi desain struktur, mengidentifikasi area yang berpotensi mengalami kegagalan, dan untuk mengoptimalkan desain struktur agar lebih kuat dan efisien.
Langkah-Langkah dalam Analisis dan Simulasi Struktur
Analisis dan simulasi struktur menggunakan matematika melibatkan serangkaian langkah yang terstruktur, seperti yang ditunjukkan pada diagram alir berikut:
| Langkah | Keterangan |
|---|---|
| 1. Pemodelan Geometri | Membuat model geometri struktur dengan menggunakan perangkat lunak pemodelan komputer. |
| 2. Definisi Bahan | Menentukan sifat material yang digunakan dalam struktur, seperti modulus elastisitas, kekuatan luluh, dan rasio Poisson. |
| 3. Definisi Kondisi Beban | Menentukan jenis dan besarnya beban yang akan bekerja pada struktur, seperti beban statis, beban dinamis, dan beban termal. |
| 4. Pemilihan Metode Analisis | Memilih metode analisis yang sesuai, seperti metode elemen hingga, metode beda hingga, atau metode elemen batas. |
| 5. Eksekusi Analisis | Melakukan analisis menggunakan perangkat lunak pemodelan komputer dan metode analisis yang dipilih. |
| 6. Interpretasi Hasil | Menganalisis hasil analisis dan mengevaluasi kekuatan, stabilitas, dan perilaku struktur. |
| 7. Optimasi Desain | Jika perlu, melakukan optimasi desain struktur untuk meningkatkan kekuatan, stabilitas, atau efisiensi. |
Implementasi Matematika dalam Konstruksi
Matematika merupakan pondasi penting dalam dunia konstruksi, berperan dalam perencanaan, pelaksanaan, dan evaluasi berbagai aspek proyek. Dari perhitungan sederhana hingga analisis kompleks, matematika membantu memastikan ketepatan, efisiensi, dan keamanan dalam setiap tahap konstruksi.
Perhitungan Volume Material dan Perencanaan Konstruksi
Matematika sangat vital dalam menentukan kebutuhan material untuk konstruksi. Melalui rumus geometri, kita dapat menghitung volume tanah, beton, baja, dan material lainnya yang dibutuhkan untuk membangun struktur. Perhitungan ini sangat penting dalam proses perencanaan konstruksi, memastikan bahwa jumlah material yang dipesan sesuai dengan kebutuhan proyek.
- Perhitungan Volume Tanah: Rumus volume kubus, balok, dan prisma digunakan untuk menghitung volume tanah yang perlu digali atau ditimbun dalam proyek konstruksi.
- Perhitungan Volume Beton: Rumus volume silinder dan balok digunakan untuk menghitung volume beton yang dibutuhkan untuk membangun kolom, balok, dan pelat lantai.
- Perhitungan Kebutuhan Baja: Rumus geometri dan persamaan kekuatan material digunakan untuk menghitung kebutuhan baja untuk struktur rangka dan penyangga.
Kontrol Kualitas dan Manajemen Proyek Konstruksi
Matematika berperan penting dalam menjaga kualitas dan kelancaran proyek konstruksi. Melalui analisis data dan pengukuran, kita dapat memastikan bahwa material yang digunakan memenuhi standar dan spesifikasi yang telah ditentukan. Selain itu, matematika juga membantu dalam memonitor kemajuan proyek, mengelola waktu dan biaya, serta mengidentifikasi potensi risiko.
- Pengukuran dan Analisis Data: Matematika digunakan untuk menganalisis data pengukuran, seperti dimensi struktur, kekuatan material, dan toleransi. Hasil analisis ini membantu dalam memastikan kualitas dan ketepatan konstruksi.
- Manajemen Waktu dan Biaya: Matematika membantu dalam perencanaan waktu dan anggaran proyek. Melalui teknik analisis dan perhitungan, kita dapat memperkirakan durasi proyek, biaya material, dan biaya tenaga kerja.
- Identifikasi Risiko: Matematika digunakan dalam analisis risiko untuk mengidentifikasi potensi masalah yang dapat terjadi selama konstruksi. Dengan memahami risiko, kita dapat mengambil langkah pencegahan yang tepat untuk meminimalkan kerugian.
Aplikasi Matematika dalam Berbagai Tahap Konstruksi
| Tahap Konstruksi | Aplikasi Matematika |
|---|---|
| Perencanaan | Geometri, Trigonometri, Aljabar, Kalkulus |
| Desain | Statika, Dinamika, Mekanika Bahan, Analisis Struktur |
| Pelaksanaan | Geometri, Trigonometri, Pengukuran, Statistik |
| Kontrol Kualitas | Statistik, Analisis Data, Pengukuran |
| Manajemen Proyek | Aljabar, Kalkulus, Statistik, Analisis Risiko |
Kesimpulan Akhir
Matematika Teknik Sipil adalah kunci untuk menciptakan dunia yang lebih baik. Dengan pemahaman yang mendalam tentang ilmu ini, para insinyur dapat merancang infrastruktur yang aman, efisien, dan berkelanjutan. Dari jembatan yang menghubungkan kota-kota hingga gedung-gedung yang menjulang tinggi, matematika menjadi bukti nyata bahwa ilmu pengetahuan dapat menciptakan keajaiban dan memajukan peradaban manusia.







